题目内容
已知幂函数f(x)=x -m2+2m+3(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(1)求函数f(x)的解析式;
(2)设函数g(x)=
(q>0),若g(x)≥0对任意x∈[1,+∞)恒成立,求实数q的取值范围.
(1)求函数f(x)的解析式;
(2)设函数g(x)=
q•
| ||
| x |
考点:函数恒成立问题,幂函数的概念、解析式、定义域、值域,幂函数的图像,幂函数图象及其与指数的关系
专题:综合题,函数的性质及应用
分析:(1)利用幂函数f(x)=x -m2+2m+3(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数,确定m的值,即可求函数f(x)的解析式;
(2)分离参数,求最值,即可求实数q的取值范围.
(2)分离参数,求最值,即可求实数q的取值范围.
解答:
解:(1)幂函数f(x)=x -m2+2m+3(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数
∴-m2+2m+3>0,∴-1<m<3,
又m∈Z,函数f(x)为偶函数,故m=1,
∴f(x)=x4;
(2)g(x)=
=
≥0对任意x∈[1,+∞)恒成立,
∴q≥-
对任意x∈[1,+∞)恒成立,
∴q≥-2,而q>0,∴q>0.
∴-m2+2m+3>0,∴-1<m<3,
又m∈Z,函数f(x)为偶函数,故m=1,
∴f(x)=x4;
(2)g(x)=
q•
| ||
| x |
| qx2+2 |
| x |
∴q≥-
| 2 |
| x2 |
∴q≥-2,而q>0,∴q>0.
点评:本题考查幂函数,考查恒成立问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
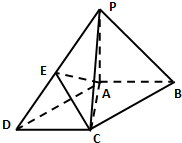 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点. 如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2
如图,已知三棱锥P-ABC,平面PAC⊥平面ABC,AB=BC=CA=4,PA=2 某个容量1000的样本的频率分布直方图如图所示,则在区间[4,5]上的数据的频数为
某个容量1000的样本的频率分布直方图如图所示,则在区间[4,5]上的数据的频数为