题目内容
设函数 =
= -sin(2x-
-sin(2x- ).
).
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2)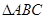 的内角
的内角 的对边分别为
的对边分别为 ,
, ,f(
,f( )=
)= ,若
,若 ,求
,求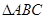 的面积.
的面积.
(1)最大值1,最小值0;(2) .
.
解析试题分析:本题考查解三角形中的正弦定理和余弦定理的运用,以及运用三角公式进行三角变换的能力和利用三角形面积求面积.第一问,先利用倍角公式和诱导公式化简表达式,再数形结合求最值;第二问,先将 代入第一问的
代入第一问的 中,得出
中,得出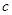 角,再利用正弦定理得到边的关系,利用余弦定理得出
角,再利用正弦定理得到边的关系,利用余弦定理得出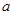 边的长,代入到三角形面积公式中即可.
边的长,代入到三角形面积公式中即可.
试题解析: (1) ,
,
∴当 时,函数取得最大值1;当
时,函数取得最大值1;当 时,函数取得最小值0 .
时,函数取得最小值0 .
(2)∵ ∴
∴ 又∵
又∵ ,
,
∴ , ∵
, ∵ , ∴
, ∴
∵ ,∴
,∴ ,
,
∴ ,∴
,∴ .
.
考点:1.倍角公式;2.诱导公式;3.正弦定理;4.余弦定理;5.三角函数的最值;6.三角形面积公式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 在R上的最大值为5.
在R上的最大值为5. 的单调递减区间。
的单调递减区间。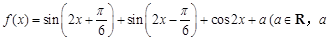 为常数).
为常数).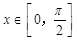 时,
时,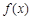 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值. .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围.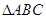 中,内角
中,内角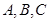 所对边长分别为
所对边长分别为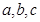 ,
,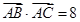 ,
,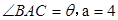 。
。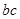 的最大值; (2)求函数
的最大值; (2)求函数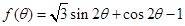 的值域.
的值域.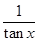 )sin2x+msin(x+
)sin2x+msin(x+ )sin(x-
)sin(x-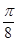 ,
, ]上的取值范围;
]上的取值范围;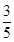 ,求m的值.
,求m的值.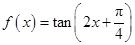 .
.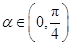 ,若
,若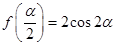 ,求
,求 的大小.
的大小.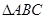 中
中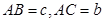 ,
, 为线段
为线段 上一点,且
上一点,且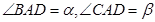 ,线段
,线段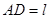 .
.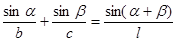 ;
;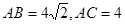 ,
,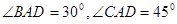 ,试求线段
,试求线段 的长.
的长.