题目内容
5.曲线y=sin x与直线x=-$\frac{π}{2}$,x=$\frac{5}{4}$π,y=0所围图形的面积为4-$\frac{\sqrt{2}}{2}$.分析 先将围成的平面图形的面积用定积分表示出来,然后运用微积分基本定理计算定积分即可.
解答 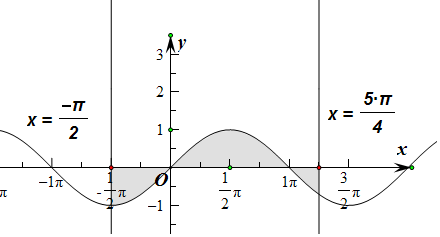 解:解:由题意和定积分的意义可得所求面积S=-${∫}_{-\frac{π}{2}}^{0}$sinxdx+${∫}_{0}^{π}$sinxdx-${∫}_{π}^{\frac{5π}{4}}$sinxdx=cosx|${\;}_{-\frac{π}{2}}^{0}$-
解:解:由题意和定积分的意义可得所求面积S=-${∫}_{-\frac{π}{2}}^{0}$sinxdx+${∫}_{0}^{π}$sinxdx-${∫}_{π}^{\frac{5π}{4}}$sinxdx=cosx|${\;}_{-\frac{π}{2}}^{0}$-
cosx|${\;}_{0}^{π}$+cosx|${\;}_{π}^{\frac{5π}{4}}$=1-(-1-1)+(-$\frac{\sqrt{2}}{2}$+1)=4-$\frac{\sqrt{2}}{2}$,
故答案为:4-$\frac{\sqrt{2}}{2}$
点评 本题主要考查了定积分在求面积中的应用,运用微积分基本定理计算定积分的关键是找到被积函数的原函数,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
17.设函数y=f(x)可导,则$\lim_{△x→0}\frac{f(1+3△x)-f(1)}{3△x}$等于( )
| A. | f'(1) | B. | 3f'(1) | C. | $\frac{1}{3}f'(1)$ | D. | 以上都不对 |
15. 根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
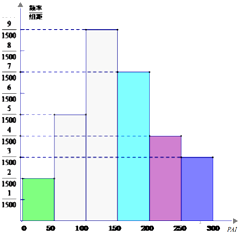
现对某城市30天的空气质量进行监测,获得30个API数据(每个数据均不同),统计绘得频率分布直方图如图.
(Ⅰ)请由频率分布直方图来估计这30天API的平均值;
(Ⅱ)若从获得的“空气质量优”和“空气质量中重度污染”的数据中随机选取2个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为$S=\left\{\begin{array}{l}0,0≤ω≤100\\ 4ω-400,100<ω≤200\\ 8ω-600,200<ω≤300\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不超过600元的概率.
 根据空气质量指数API(为整数)的不同,可将空气质量分级如表:
根据空气质量指数API(为整数)的不同,可将空气质量分级如表:| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 |
(Ⅰ)请由频率分布直方图来估计这30天API的平均值;
(Ⅱ)若从获得的“空气质量优”和“空气质量中重度污染”的数据中随机选取2个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为$S=\left\{\begin{array}{l}0,0≤ω≤100\\ 4ω-400,100<ω≤200\\ 8ω-600,200<ω≤300\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不超过600元的概率.