题目内容
关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,则m的取值范围为( )
| A、∅ | ||
| B、(-∞,-1) | ||
C、(
| ||
D、(-
|
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:令f(x)=mx2+2(m+3)x+2m+14,则由题意可得
①,或
②,分别求得①、②的解集,再取并集,即得所求.
|
|
解答:
解:令f(x)=mx2+2(m+3)x+2m+14,则由题意可得
①,或
②.
解①求得m∈∅,解②求得-
<m<0,
故选:D.
|
|
解①求得m∈∅,解②求得-
| 19 |
| 13 |
故选:D.
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若f(x)=x5+2x3+3x2+x+1,用秦九韶算法计算f(3)=( )
| A、327 | B、328 |
| C、165 | D、166 |
从只含有二件次品的10个产品中取出三件,设A为“三件产品不全是次品”,B为“三件产品全不是次品”,C为“三件产品全是次品”,则下列结论正确的是( )
| A、事件A与B互斥 |
| B、事件A是随机事件 |
| C、任两个均互斥 |
| D、事件C是不可能事件 |
已知等差数列{an}满足a2+a10=4,则a6=( )
| A、-2 | B、2 | C、4 | D、-4 |

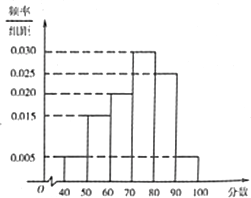 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为