题目内容
已知函数f(x)=-sin2x+sinx+a,
(1)当f(x)=0有实数解时,求a的取值范围;(2)若x∈R,有1≤f(x)≤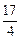 ,求a的取值范围。
,求a的取值范围。
(1)当f(x)=0有实数解时,求a的取值范围;(2)若x∈R,有1≤f(x)≤
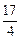 ,求a的取值范围。
,求a的取值范围。(1)a∈[ ,2] (2)3≤a≤4
,2] (2)3≤a≤4
 ,2] (2)3≤a≤4
,2] (2)3≤a≤4(1)f(x)=0,即a=sin2x-sinx=(sinx- )2-
)2-
∴当sinx= 时,amin=
时,amin= ,当sinx=-1时,amax=2,
,当sinx=-1时,amax=2,
∴a∈[ ,2]为所求
,2]为所求
(2)由1≤f(x)≤ 得
得
∵ u1=sin2x-sinx+ +4≥4
+4≥4
u2=sin2x-sinx+1= ≤3
≤3
∴ 3≤a≤4
 )2-
)2-
∴当sinx=
 时,amin=
时,amin= ,当sinx=-1时,amax=2,
,当sinx=-1时,amax=2,∴a∈[
 ,2]为所求
,2]为所求(2)由1≤f(x)≤
 得
得
∵ u1=sin2x-sinx+
 +4≥4
+4≥4u2=sin2x-sinx+1=
 ≤3
≤3∴ 3≤a≤4

练习册系列答案
相关题目
 =
= ,求证:a+
,求证:a+
 ,
, 相邻两对称轴间的距离大于等于
相邻两对称轴间的距离大于等于
 的取值范围;
的取值范围;

 的面积.
的面积. ,
, ,函数
,函数 .
. 的最大值及相应的
的最大值及相应的 的值;(Ⅱ) 若
的值;(Ⅱ) 若 ,求
,求 的值.
的值.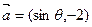 与
与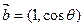 互相垂直,其中
互相垂直,其中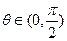 .
.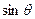 和
和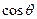 的值;(2)若
的值;(2)若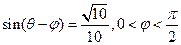 ,求
,求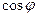 的值.
的值.  ;
; ,
, 的面积
的面积 ,求
,求 的值
的值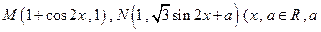 是常数
是常数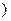 ,令
,令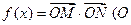 是坐标原点
是坐标原点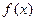 的解析式,并求函数
的解析式,并求函数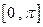 上的单调递增区间;
上的单调递增区间;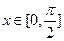 时,
时,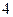 ,求a的值,并说明此时
,求a的值,并说明此时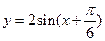 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到? ,求
,求 的值。
的值。 的图象关于直线
的图象关于直线 对称,当
对称,当 ,
,  时,试求
时,试求 的值.
的值.