题目内容
1．已知函数f（x）=x2-（c+1）x+c（c∈R）．（1）解关于x的不等式f（x）＜0；
（2）当c=1时，不等式f（x）＞a-5在（0，2）上恒成立，求实数a的取值范图；
（3）设g（x）=f（x）-x2-（a-1）x，已知0＜g（2）＜1，3＜g（3）＜5．求g（4）-a的范图．
分析 （1）因式分解，对c分类写出不等式的解集；
（2）根据恒成立问题转换为最值问题，只需求出在（0，2）上最小值即可；
（3）分别求出g（3），g（4），g（5）-a，得出g（4）-a=-5a-3c=g（2）+g（3），求解即可．
解答 解：（1）f（x）=x2-（c+1）x+c＜0，
∴（x-c）（x-1）＜0，
当c＞1时，1＜x＜c；
当c＜1时，c＜x＜1；
当c=1时，无解；
（2）当c=1时，不等式f（x）＞a-5在（0，2）上恒成立，
∴（x-1）2＞a-5在（0，2）上恒成立，
∴0＞a-5，
∴a＜5；
（3）g（x）=f（x）-x2-（a-1）x
=-（a+c）x+c，
∴g（2）=-2a-c，
g（3）=-3a-2c
g（4）-a=-5a-3c=g（2）+g（3），
∴3＜g（4）-a＜6．
点评 考查了二次不等式的分类和恒成立问题的转换．
练习册系列答案
相关题目
11．
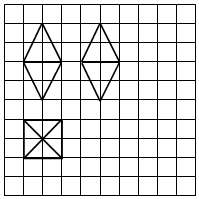如图，网格纸上正方形小格的边长为1个单位长度，图中粗线曲出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上正方形小格的边长为1个单位长度，图中粗线曲出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | 16 | B． | 8$\sqrt{5}$ | C． | 32 | D． | 16$\sqrt{5}$ |
12．曲线y=e${\;}^{\frac{1}{3}x}$在点（6，e2）处的切线与坐标轴所围成的三角形的面积为（ ）
| A． | $\frac{3}{2}{e}^{2}$ | B． | 3e2 | C． | 6e2 | D． | 9e2 |
9．某公司为了增加其商品的销售利润，调查了该商品投入的广告费用x与销售利润y的统计数据如表：
由表中数据，得线性回归方程l：$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$（$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$x），则下列结论错误的是（ ）
| 广告费用x（万元） | 2 | 3 | 5 | 6 |
| 销售利润y（万元） | 5 | 7 | 9 | 11 |
| A． | $\hat b＞0$ | B． | $\hat a＞0$ | C． | 直线l过点（4，8） | D． | 直线l过点（2，5） |
11．已知数列{an}、{bn}满足an=$\frac{n}{2}$${•b}_{n}+{2}^{n-1}•{b}_{n+1}$，bn=1-（-1）n，设数列{an}前n项和为Sn，则S2016的值为（ ）
| A． | 10082+2（21008-1） | B． | 1007×1008+2（21008-1） | ||
| C． | 10082+$\frac{4}{3}$（41008-1） | D． | 1007×1008+$\frac{4}{3}$（41008-1） |