题目内容
【题目】已知椭圆C:![]() (
(![]() )的长轴长是短轴长的2倍,左焦点为
)的长轴长是短轴长的2倍,左焦点为![]() .
.
(1)求C的方程;
(2)设C的右顶点为A,不过C左、右顶点的直线l:![]() 与C相交于M,N两点,且
与C相交于M,N两点,且![]() .请问:直线l是否过定点?如果过定点,求出该定点的坐标;如果不过定点,请说明理由.
.请问:直线l是否过定点?如果过定点,求出该定点的坐标;如果不过定点,请说明理由.
【答案】(1)![]() ;(2)是,
;(2)是,![]() .
.
【解析】
(1)由焦点坐标、长轴长和短轴长关系、椭圆![]() 关系可构造方程组求得
关系可构造方程组求得![]() ,进而得到所求方程;
,进而得到所求方程;
(2)将直线方程与椭圆方程联立,得到韦达定理的形式;根据垂直关系可得![]() ,代入韦达定理的结果可整理得到
,代入韦达定理的结果可整理得到![]() ,进而解得
,进而解得![]() ,
,![]() ;分别验证两个结果可知
;分别验证两个结果可知![]() 满足题意,根据直线过定点的求解方法可确定定点坐标.
满足题意,根据直线过定点的求解方法可确定定点坐标.
(1)由题意得: ,解得:
,解得:![]()
![]() 的方程为:
的方程为:![]()
(2)设![]() ,
,![]()
由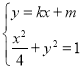 得:
得:![]()
则![]() ,化简得:
,化简得:![]() …①
…①
![]() ,
,![]()
又![]()
![]()
![]() ,即
,即![]()
又![]()
![]()
即![]()
化简为:![]()
解得:![]() ,
,![]() ,均满足①式
,均满足①式
当![]() 时,
时,![]() ,直线
,直线![]() 过点
过点![]() ,不合题意,舍去;
,不合题意,舍去;
当![]() 时,
时,![]() ,直线
,直线![]() 过定点
过定点![]()
综上可知,直线![]() 过定点,定点坐标为
过定点,定点坐标为![]()

练习册系列答案
相关题目
【题目】某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为![]() ,对该款智能家电的评分为
,对该款智能家电的评分为![]() .若根据统计数据,用最小二乘法得到
.若根据统计数据,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,且年龄
,且年龄![]() 的方差为
的方差为![]() ,评分
,评分![]() 的方差为
的方差为![]() .求
.求![]() 与
与![]() 的相关系数
的相关系数![]() ,并据此判断对该款智能家电的评分与年龄的相关性强弱.
,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有![]() 的把握认为对该智能家电的评价与年龄有关.
的把握认为对该智能家电的评价与年龄有关.
好评 | 差评 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:线性回归直线![]() 的斜率
的斜率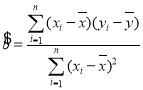 ;相关系数
;相关系数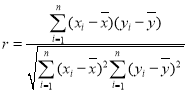 ,独立性检验中的
,独立性检验中的![]() ,其中
,其中![]() .
.
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |