题目内容
【题目】为了解某中学学生对数学学习的情况，从该校抽了
名学生，分析了这名学生某次数学考试成绩（单位：分），得到了如下的频率分布直方图：
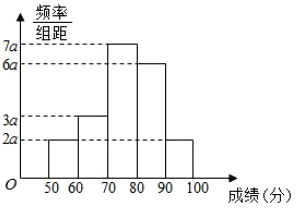
（1）求频率分布直方图中
的值；
（2）根据频率分布直方图估计该组数据的中位数（精确到
）；
（3）在这名学生的数学成绩中，从成绩在
的学生中任选
人，求次人的成绩都在
中的概率．
【答案】（1）
（2）7.7（3）
【解析】
（1）由直方图知
，由此能求出
；
（2）由频率分布直方图中的中位数为频率为0.5对应的横坐标，即可能估计高二数学成绩的中位数；
（3）记成绩落在
，
中的2人为
，
，成绩落在
，
中的3人为
，
，
，从成绩在，的学生中任选2人，利用列举法能求出2人的成绩都在，中的概率．
（1）由直方图可得：
，解得：.
（2）该组数据的中位数：
.
（3）成绩在
有
人，记为
，
，成绩在
有
人，记为
，
，
设事件
为“人的成绩都在中”，所有的基本事件为：
，
，
，
，
，
，
，
，
，
共
种，
满足条件的基本事件为：，，共3种
，故人的成绩都在中的概率为.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某集团公司为了加强企业管理，树立企业形象，考虑在公司内部对迟到现象进行处罚.现在员工中随机抽取200人进行调查，当不处罚时，有80人会迟到，处罚时，得到如下数据：
处罚金额 | 50 | 100 | 150 | 200 |
迟到的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
（Ⅰ）当处罚金定为100元时，员工迟到的概率会比不进行处罚时降低多少？
（Ⅱ）将选取的200人中会迟到的员工分为
，
两类：类员工在罚金不超过100元时就会改正行为；类是其他员工.现对类与类员工按分层抽样的方法抽取4人依次进行深度问卷，则前两位均为类员工的概率是多少？
