题目内容
16.若关于x的不等式a-ax>ex(2x-1)(a>-1)有且仅有两个整数解,则实数a的取值范围为( )| A. | (-$\frac{3}{4}$,$\frac{5}{3{e}^{2}}$] | B. | (-1,$\frac{3}{2e}$] | C. | (-$\frac{3}{2e}$,-$\frac{5}{3{e}^{2}}$] | D. | (-$\frac{3}{4}$,-$\frac{5}{3{e}^{2}}$) |
分析 构造函数,作出两个函数的图象得到不等式关系进行求解即可.
解答 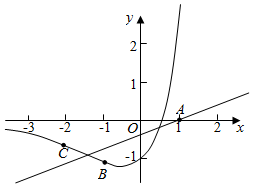 解:由a-ax>ex(2x-1)(a>-1),
解:由a-ax>ex(2x-1)(a>-1),
设g(x)=a-ax,h(x)=ex(2x-1),
h′(x)=ex(2x-1)+2ex=ex(2x+1),
由h′(x)>0得x>-$\frac{1}{2}$,
由h′(x)<0得x<-$\frac{1}{2}$,
即当x=-$\frac{1}{2}$时,函数h(x)取得极小值h(-$\frac{1}{2}$),
作出g(x)的图象如图:
若g(x)>h(x)解集中的整数恰为2个,
则x=0,-1是解集中的两个整数,
则满足$\left\{\begin{array}{l}{g(-1)>h(-1)}\\{g(-2)≤h(-2)}\end{array}\right.$,即$\left\{\begin{array}{l}{2a>\frac{-3}{e}}\\{3a≤\frac{-5}{{e}^{2}}}\end{array}\right.$,
则$\left\{\begin{array}{l}{a>\frac{-3}{2e}}\\{a≤-\frac{5}{3{e}^{2}}}\end{array}\right.$,即-$\frac{3}{2e}$<a≤-$\frac{5}{3{e}^{2}}$,
即实数a的取值范围是(-$\frac{3}{2e}$,-$\frac{5}{3{e}^{2}}$],
故选:C
点评 本题主要考查函数与方程的应用,根据不等式整数根的个数,结合数形结合建立不等式关系是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
7.已知函数y=f(x)=|x-1|-mx,若关于x的不等式f(x)<0解集中的整数恰为3个,则实数m的取值范围为 ( )
| A. | $\frac{2}{3}<m≤\frac{3}{4}$ | B. | $\frac{3}{4}<m≤\frac{4}{5}$ | C. | $\frac{2}{3}<m<\frac{3}{4}$ | D. | $\frac{3}{4}<m<\frac{4}{5}$ |
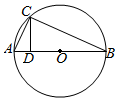 圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.
圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.