题目内容
17.已知$z=a+\sqrt{3}i$(a>0)且|z|=2,则$\overline z$=( )| A. | $1-\sqrt{3}i$ | B. | $1+\sqrt{3}i$ | C. | $2-\sqrt{3}i$ | D. | $3+\sqrt{3}i$ |
分析 由已知利用复数模的计算公式求得a,则$\overline{z}$可求.
解答 解:∵$z=a+\sqrt{3}i$(a>0)且|z|=2,
∴$\sqrt{{a}^{2}+3}=2$,解得a=1,
∴z=1+$\sqrt{3}i$,
则$\overline{z}=1-\sqrt{3}i$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查复数模的求法,是基础题.

练习册系列答案
相关题目
7.如图所示,两个阴影部分的面积之和可表示为( )
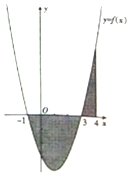

| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
5.某地区的年降水量在下列范围内的概率如表所示:
则年降水量在[200,300](mm)范围内的概率为0.51,年降水量在[300,400](mm)范围内的概率为0.22.
| 年降水量(mm) | [200,250] | [250,300] | [300,350] | [350,400] |
| 概率 | 0.30 | 0.21 | 0.14 | 0.08 |
12.若实数x,y满足条件$\left\{\begin{array}{l}x-1≤0\\ x-y≥-1\\ 2x+y≥2\end{array}\right.$,则$z=-\frac{3}{4x+3y}$的最大值为( )
| A. | $-\frac{9}{16}$ | B. | $-\frac{3}{4}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{1}{4}$ |
2.已知三角形ABC的边BC中点为D,且G点满足$\overrightarrow{GA}+\overrightarrow{BG}+\overrightarrow{CG}=\overrightarrow 0$,且$\overrightarrow{AG}=λ\overrightarrow{GD}$,则λ的值是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
7.若x、y满足$\left\{\begin{array}{l}x+y-2≥0\\ kx-y+2≥0\\ y≥0\end{array}\right.$,且z=y-x的最小值为-6,则k的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
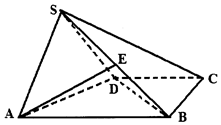 已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.
已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.