题目内容
1.已知向量$\vec a=(2,-3,1),\vec b=(-4,2,x)$,且$\vec a⊥\vec b$,则x的值为( )| A. | 12 | B. | 10 | C. | -14 | D. | 14 |
分析 利用空间向量的数量积公式以及向量垂直的性质得到关于x的方程解之即可.
解答 解:因为向量$\vec a=(2,-3,1),\vec b=(-4,2,x)$,且$\vec a⊥\vec b$,
属于$\overrightarrow{a}•\overrightarrow{b}$=-8-6+x=0,解得x=14;
故选:D.
点评 本题考查了空间向量的数量积以及向量垂直的性质;属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
12.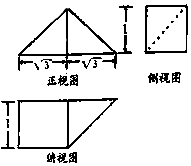 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的体积( )| A. | $\frac{{5\sqrt{3}}}{6}$ | B. | $\frac{{7\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{3\sqrt{3}}}{6}$ |
13.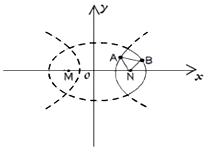 有一凸透镜其剖面图(如图)是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(a>m>0)的实线部分组成,已知两曲线有共同焦点M、N;A、B分别在左右两部分实线上运动,则△ANB周长的最小值为( )
有一凸透镜其剖面图(如图)是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(a>m>0)的实线部分组成,已知两曲线有共同焦点M、N;A、B分别在左右两部分实线上运动,则△ANB周长的最小值为( )
 有一凸透镜其剖面图(如图)是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(a>m>0)的实线部分组成,已知两曲线有共同焦点M、N;A、B分别在左右两部分实线上运动,则△ANB周长的最小值为( )
有一凸透镜其剖面图(如图)是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(a>m>0)的实线部分组成,已知两曲线有共同焦点M、N;A、B分别在左右两部分实线上运动,则△ANB周长的最小值为( )| A. | 2(a-m) | B. | (a-m) | C. | 2(b-n) | D. | 2(a+m) |
10.F1,F2分别是双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 4$\sqrt{2}$ |
11.各项均为正数的等比数列{an}的前n项和为Sn,若S4=10,S12=130,则S8=( )
| A. | -30 | B. | 40 | C. | 40或-30 | D. | 40或-50 |
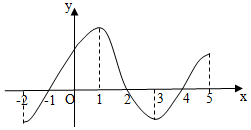 如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).
如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).



