题目内容
8．已知x，y满足不等式组$\left\{\begin{array}{l}y-1≥0\\ x-y+2≥0\\ x+4y-8≤0\end{array}\right.$则目标函数z=2x+y的最大值为9．分析 画出约束条件表示的可行域，判断目标函数z=2x+y的位置，求出最大值．
解答 
解：作出不等式组$\left\{\begin{array}{l}y-1≥0\\ x-y+2≥0\\ x+4y-8≤0\end{array}\right.$的可行域如图，
目标函数z=2x+y在$\left\{\begin{array}{l}{y=1}\\{x+4y-8=0}\end{array}\right.$的交点A（4，1）处取最大值为z=2×4+1=9．
故答案为：9．
点评 本题考查简单的线性规划的应用，正确画出可行域，判断目标函数经过的位置是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．设$f（x）=\sqrt{3}sinωx-cosωx（ω＞0）$的最小正周期为π，则f（x）的一个单调递减区间是（ ）
| A． | $（-\frac{π}{2}，0）$ | B． | $（-\frac{π}{6}，\frac{π}{3}）$ | C． | $（\frac{π}{3}，\frac{5π}{6}）$ | D． | $（\frac{π}{2}，π）$ |
19．如表是x，y的对应数据，由表中数据得线性回归方程为$\stackrel{∧}{y}$=0.8x-$\stackrel{∧}{a}$．那么，当x=60时，相应的$\stackrel{∧}{y}$为（ ）
| x | 15 | 20 | 25 | 30 | 35 |
| y | 6 | 12 | 14 | 20 | 23 |
| A． | 38 | B． | 43 | C． | 48 | D． | 52 |
16．已知x2+y 2=1，若x+y-k≥0对符合条件一切x、y都成立，则实数k的最大值为（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | 0 | D． | 1 |
3．若a+a-1=3，则a2+a-2的值为（ ）
| A． | 9 | B． | 7 | C． | 6 | D． | 4 |
20．已知角a的终边经过点P（-4，m），且$sinα=\frac{3}{5}$，则m等于（ ）
| A． | 3 | B． | $\frac{3}{5}$ | C． | -3 | D． | $-\frac{3}{5}$ |
17．函数$y=sin\frac{1}{2}x$（ ）
| A． | 在[-π，π]上是增函数 | B． | 在[0，π]上是减函数 | ||
| C． | 在$[{-\frac{π}{2}，\frac{π}{2}}]$上是减函数 | D． | 在[-π，0]上是减函数 |
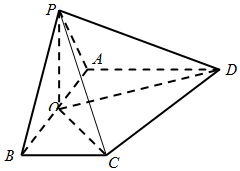如图，已知在四棱锥P-ABCD中，O为AB中点，平面POC⊥平面ABCD，AD∥BC，AB⊥BC，PA=PB=BC=AB=2，AD=3