题目内容
1.某调研机构调取了当地2014年10月~2015年3月每月的雾霾天数与严重交通事故案例数资料进行统计分析,以备下一年如何预防严重交通事故作参考.部分资料如下:| 时间 | 14年10月 | 14年11月 | 14年12月 | 15年1月 | 15年2月 | 15年3月 |
| 雾霾天数 | 7 | 11 | 13 | 12 | 10 | 8 |
| 严重交通事故案例数 | 14 | 25 | 29 | 26 | 22 | 16 |
(1)求剔除的2组数据不是相邻2个月数据的概率;
(2)若剔除的是2014年10月与2015年2月这两组数据,请你根据其它4个月的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)①根据(2)所求的回归方程,求2014年10月与2015年2月的严重交通事故案例数;
②判断(2)所求的线性回归方程是否是合情的.
[附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)代入古典概型的概率公式计算;
(2)根据回归系数公式计算回归系数,得出回归方程;
(3)利用回归方程进行估计,检验.
解答 解:(1)剔除的2组数据不是相邻2个月的数据概率为P=1-$\frac{5}{{C}_{6}^{2}}$=$\frac{2}{3}$.
(2)$\overline{x}=\frac{11+13+12+8}{4}=11$,$\overline{y}=\frac{25+29+26+16}{4}=24$.
∴$\stackrel{∧}{b}$=$\frac{(11×25+13×29+12×26+8×16)-4×11×24}{1{1}^{2}+1{3}^{2}+1{2}^{2}+{8}^{2}-4×1{1}^{2}}$=$\frac{18}{7}$,$\stackrel{∧}{a}$=$24-\frac{18}{7}×11$=-$\frac{30}{7}$.
∴x的线性回归方程$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$.
(3)①当x=7时,$\widehat{y}$=$\frac{96}{7}$,当x=10时,$\widehat{y}$=$\frac{150}{7}$.
②当x=7时,|$\frac{96}{7}-14$|=$\frac{2}{7}$<2;
当x=10时,|$\frac{150}{7}-22$|=$\frac{4}{7}<2$.
∴线性回归方程是合情的.
点评 本题考查了线性回归方程的求解,古典概型的概率计算,属于基础题.

练习册系列答案
相关题目
16.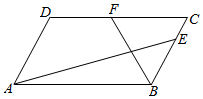 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )| A. | $-\frac{8}{3}$ | B. | -1 | C. | 2 | D. | $\frac{10}{3}$ |
9.若复数z=i-2i2+3i3,则|z|=( )
| A. | 6 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
16.设α为锐角,则“log2tanα>1”是“0<sin2α<$\frac{4}{5}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知m>0,n>0,在(1+mx)3+(1+$\sqrt{3}$nx)2的展开式中,当x2项系数为3时,则m+n的最大值为( )
| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
10.已知单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足2$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2,设$\overrightarrow{OP}=x\overrightarrow{a}+y\overrightarrow{b}$,若x,y满足$\left\{\begin{array}{l}{x+y≥1}\\{x≥0}\\{y≥0}\end{array}\right.$,则|$\overrightarrow{OP}$|的最小值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
 正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.
正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.