题目内容
12.在掷均匀硬币的试验中,以下对“大数定理”的理解错误的是( )| A. | 大量的试验中,出现正面的频率稳定于$\frac{1}{2}$ | |
| B. | 不管试验多少次,出现正面的概率始终为$\frac{1}{2}$ | |
| C. | 试验次数增多,出现正面的经验概率越接近$\frac{1}{2}$ | |
| D. | 试验次数无限增大时,出现正面的频率的极限为$\frac{1}{2}$ |
分析 大数定律(law of large numbers),是一种描述当试验次数很大时所呈现的概率性质的定律.但是注意到,大数定律并不是经验规律,而是在一些附加条件上经严格证明了的定理,它是一种自然规律因而通常不叫定理而是大数“定律”,
解答 解:在重复投掷一枚硬币的随机试验中,观测投掷了n次硬币中出现正面的次数,不同的n次试验,出现正面的频率(出现正面次数与n之比)可能不同,但当试验的次数n越来越大时,出现正面的频率将大体上逐渐接近于$\frac{1}{2}$,
故选:B.
点评 本题考查了“大数定理”的概念,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4.下列等式恒成立的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | ($\overrightarrow{a}•\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}•\overrightarrow{c}$) | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$ |
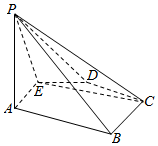 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.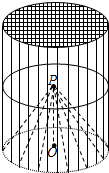 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.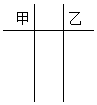 某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下:
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩如下: