题目内容
11.已知函数f(x)=asinx+ln(1-x).(1)若a=1,求f(x)在x=0处的切线方程;
(2)若f(x)在区间[0,1)上单调递减,求a的取值范围;
(3)求证:e${\;}^{sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}}$<2,(n∈N*).
分析 (1)把a=1代入函数解析式,求出导函数,得到f′(0)及f(0),然后利用直线方程的点斜式得答案;
(2)由f(x)在区间[0,1)上单调递减,可得f′(x)=acosx-$\frac{1}{1-x}$≤0对x∈[0,1)恒成立,然后对a分类即可求得a的取值范围为(-∞,1];
(3)由(2)知,当a=1时,f(x)=sinx+ln(1-x)在(0,1)上单调递减,可得f(x)<f(0)=0,即sinx<ln$\frac{1}{1-x}$,由$sin\frac{1}{(n+1)^{2}}$<$ln\frac{1}{1-\frac{1}{(n+1)^{2}}}=ln\frac{(n+1)^{2}}{n(n+2)}$及$ln\frac{{2}^{2}}{1•3}+ln\frac{{3}^{2}}{2•4}+…+ln\frac{(n+1)^{2}}{n(n+2)}$=ln[$\frac{{2}^{2}}{1•3}•\frac{{3}^{2}}{2•4}…\frac{(n+1)^{2}}{n(n+2)}$]=$ln\frac{2(n+1)}{n+2}=ln[2(1-\frac{1}{n+2})]$<ln2.即可证得$sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}$<ln2.则e${\;}^{sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}}$<2,(n∈N*).
解答 (1)解:a=1时,f(x)=asinx+ln(1-x),
f′(x)=cosx-$\frac{1}{1-x}$,∴f′(0)=0,又f(0)=0,
∴f(x)在x=0处的切线方程为y=0;
(2)解:∵f(x)在区间[0,1)上单调递减,
∴f′(x)=acosx-$\frac{1}{1-x}$≤0对x∈[0,1)恒成立,
若a≤0,x∈[0,1)时,acosx-$\frac{1}{1-x}$≤0成立.
若a>0,acosx-$\frac{1}{1-x}$≤0?(1-x)cosx$≤\frac{1}{a}$.
令h(x)=(1-x)cosx,显然h(x)在[0,1)上单调递减,
∴h(x)≤h(0)=1,∴$\frac{1}{a}≥1$,则0<a≤1.
综上,a的取值范围为(-∞,1];
(3)证明:由(2)知,当a=1时,f(x)=sinx+ln(1-x)在(0,1)上单调递减,
∴f(x)<f(0)=0,即sinx<ln$\frac{1}{1-x}$,
而$\frac{1}{(n+1)^{2}}$∈(0,1),∴$sin\frac{1}{(n+1)^{2}}$<$ln\frac{1}{1-\frac{1}{(n+1)^{2}}}=ln\frac{(n+1)^{2}}{n(n+2)}$,
∴$sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}$<$ln\frac{{2}^{2}}{1•3}+ln\frac{{3}^{2}}{2•4}+…+ln\frac{(n+1)^{2}}{n(n+2)}$,
而$ln\frac{{2}^{2}}{1•3}+ln\frac{{3}^{2}}{2•4}+…+ln\frac{(n+1)^{2}}{n(n+2)}$=ln[$\frac{{2}^{2}}{1•3}•\frac{{3}^{2}}{2•4}…\frac{(n+1)^{2}}{n(n+2)}$]=$ln\frac{2(n+1)}{n+2}=ln[2(1-\frac{1}{n+2})]$<ln2.
∴$sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}$<ln2.
∴e${\;}^{sin\frac{1}{(1+1)^{2}}+sin\frac{1}{(2+1)^{2}}+…+sin\frac{1}{(n+1)^{2}}}$<2,(n∈N*).
点评 本题考查利用导数求过曲线上某点处的切线方程,考查利用导数研究函数的单调性,训练了由导数及放缩法证明函数不等式,是压轴题.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案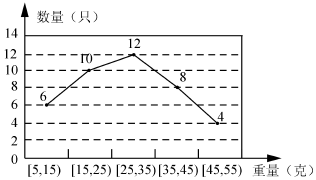
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)试估计这批小龙虾的平均重量;
(3)为适应市场需求,制定促销策略.该经销商又将这批小龙虾分成三个等级,并制定出销售单价,如下表:
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,35) | [35,55] |
| 单价(元/只) | 1.2 | 1.5 | 1.8 |
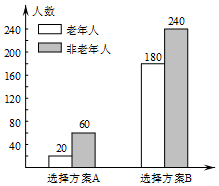 为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:
为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:(Ⅰ)根据已知条件完成下面的2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关?
| 选择方案A | 选择方案B | 总计 | |
| 老年人 | |||
| 非老年人 | |||
| 总计 | 500 |
(Ⅱ)根据(Ⅰ)的结论,能否提出一个更好的调查方法,使得调查结果更具代表性,说明理由.
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |