题目内容
 已知椭圆C1:
已知椭圆C1: 的离心率为
的离心率为 ,椭圆上一点到一个焦点的最大值为3,圆
,椭圆上一点到一个焦点的最大值为3,圆 ,点A是椭圆上的顶点,点P是椭圆C1上不与椭圆顶点重合的任意一点.
,点A是椭圆上的顶点,点P是椭圆C1上不与椭圆顶点重合的任意一点.
(1)求椭圆C1的方程;
(2)若直线AP与圆C2相切,求点P的坐标;
(3)若点M是椭圆C1上不与椭圆顶点重合且异于点P的任意一点,点M关于x轴的对称点是点N,直线MP,NP分别交x轴于点E(x1,0),点F(x2,0),探究x1•x2是否为定值.若为定值,求出该定值;若不为定值,请说明理由.
解:(1)由题意, ,∴a=2,c=1,∴b2=a2-c2=3,∴椭圆C1的方程为
,∴a=2,c=1,∴b2=a2-c2=3,∴椭圆C1的方程为 ;
;
(2)由(1)知A(0, ),且直线AP的斜率存在,设其斜率为k,则直线AP的方程为kx-y+
),且直线AP的斜率存在,设其斜率为k,则直线AP的方程为kx-y+ =0
=0
圆C2的圆心坐标为(-4, ),半径为2
),半径为2
∵直线AP与圆C2相切,
∴ =2
=2
∴
k= 时,直线方程代入椭圆方程可得5x2+8x=0,∴x=0或x=-
时,直线方程代入椭圆方程可得5x2+8x=0,∴x=0或x=- ,∴点P的坐标为(-
,∴点P的坐标为(- ,-
,-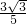 )
)
同理可得k=- 时,点P的坐标为(
时,点P的坐标为( ,-
,-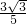 );
);
(3)设M(x3,y3),P(x4,y4),则N(x3,-y3),
由M,P,E三点共线,可得 =
= ,∴
,∴
同理由N,P,F三点共线,可得
∵M,P在椭圆上,∴ ,
,
∴x1•x2= ×
× =4
=4
∴x1•x2是定值,定值为4.
分析:(1)根据的离心率为 ,椭圆上一点到一个焦点的最大值为3,建立方程组,即可求得椭圆C1的方程;
,椭圆上一点到一个焦点的最大值为3,建立方程组,即可求得椭圆C1的方程;
(2)设直线AP的方程为kx-y+ =0,利用直线AP与圆C2相切,求得直线的斜率,从而可得点P的坐标;
=0,利用直线AP与圆C2相切,求得直线的斜率,从而可得点P的坐标;
(3)设M、P、N的坐标,利用M,P,E三点共线,N,P,F三点共线,结合M,P在椭圆上,即可求得x1•x2是定值.
点评:本题考查椭圆的标准方程,考查直线与圆相切,考查三点共线,正确确定椭圆方程是关键.
 ,∴a=2,c=1,∴b2=a2-c2=3,∴椭圆C1的方程为
,∴a=2,c=1,∴b2=a2-c2=3,∴椭圆C1的方程为 ;
;(2)由(1)知A(0,
 ),且直线AP的斜率存在,设其斜率为k,则直线AP的方程为kx-y+
),且直线AP的斜率存在,设其斜率为k,则直线AP的方程为kx-y+ =0
=0圆C2的圆心坐标为(-4,
 ),半径为2
),半径为2
∵直线AP与圆C2相切,
∴
 =2
=2
∴

k=
 时,直线方程代入椭圆方程可得5x2+8x=0,∴x=0或x=-
时,直线方程代入椭圆方程可得5x2+8x=0,∴x=0或x=- ,∴点P的坐标为(-
,∴点P的坐标为(- ,-
,-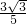 )
)同理可得k=-
 时,点P的坐标为(
时,点P的坐标为( ,-
,-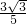 );
);(3)设M(x3,y3),P(x4,y4),则N(x3,-y3),
由M,P,E三点共线,可得
 =
= ,∴
,∴
同理由N,P,F三点共线,可得

∵M,P在椭圆上,∴
 ,
,
∴x1•x2=
 ×
× =4
=4∴x1•x2是定值,定值为4.
分析:(1)根据的离心率为
 ,椭圆上一点到一个焦点的最大值为3,建立方程组,即可求得椭圆C1的方程;
,椭圆上一点到一个焦点的最大值为3,建立方程组,即可求得椭圆C1的方程;(2)设直线AP的方程为kx-y+
 =0,利用直线AP与圆C2相切,求得直线的斜率,从而可得点P的坐标;
=0,利用直线AP与圆C2相切,求得直线的斜率,从而可得点P的坐标;(3)设M、P、N的坐标,利用M,P,E三点共线,N,P,F三点共线,结合M,P在椭圆上,即可求得x1•x2是定值.
点评:本题考查椭圆的标准方程,考查直线与圆相切,考查三点共线,正确确定椭圆方程是关键.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.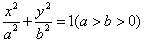 的离心率为
的离心率为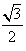 ,x轴被抛物线C2:y=x2-b截得的线段长等于C1的长半轴长,
,x轴被抛物线C2:y=x2-b截得的线段长等于C1的长半轴长,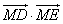 为定值;
为定值; 的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,
,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,  的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。  的离心率为
的离心率为 ,椭圆上一点到一个焦点的最大值为3,圆
,椭圆上一点到一个焦点的最大值为3,圆 ,点A是椭圆上的顶点,点P是椭圆C1上不与椭圆顶点重合的任意一点.
,点A是椭圆上的顶点,点P是椭圆C1上不与椭圆顶点重合的任意一点.