题目内容
17．
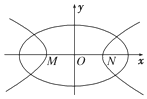如图，中心均为原点O的椭圆与双曲线有公共焦点，M，N是双曲线的两顶点．若M，O，N将椭圆长轴四等分，则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$．
分析 根据M，N是双曲线的两顶点，M，O，N将椭圆长轴四等分，可得椭圆的长轴长是双曲线实轴长的2倍，利用双曲线与椭圆有公共焦点，即可求得双曲线与椭圆的离心率的比值．
解答 解：∵M，N是双曲线的两顶点，M，O，N将椭圆长轴四等分
∴椭圆的长轴长是双曲线实轴长的2倍
∵双曲线与椭圆有公共焦点，
∴双曲线与椭圆的离心率的比值是2
椭圆与双曲线的离心率的比值是为：$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查椭圆、双曲线的几何性质，解题的关键是确定椭圆的长轴长是双曲线实轴长的2倍．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
5．为得到函数y=cos2x的图象，只需将$y=cos（2x+\frac{π}{6}）$函数的图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{12}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
2．已知cos（α+$\frac{π}{4}$）=$\frac{3}{5}$，$\frac{π}{2}$$≤α≤\frac{3π}{2}$，则sin2α=（ ）
| A． | -$\frac{4}{5}$ | B． | $\frac{4}{5}$ | C． | -$\frac{7}{25}$ | D． | $\frac{7}{25}$ |
9．积分$\int_1^e{（\frac{1}{x}+2x）dx}$的值为（ ）
| A． | 1 | B． | e | C． | e+1 | D． | e2 |
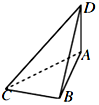如图，在正三棱柱ABC-A1B1C1中，D为棱AA1的中点．若截面△BC1D是面积为6的直角三角形，则此三棱柱的体积为$8\sqrt{3}$．