题目内容
19.抛物线x2=ay上有一点A(x0,2),它到焦点的距离是3,则其标准方程是( )| A. | x2=y | B. | x2=2y | C. | x2=3y | D. | x2=4y |
分析 求得抛物线的焦点坐标,利用焦点弦公式即可求得a的值,求得a抛物线方程.
解答 解:抛物线的x2=ay,焦点坐标F(0,$\frac{a}{4}$),准线方程为y=-$\frac{a}{4}$,
由抛物线的焦点弦公式可知:A到焦点F的距离丨AF丨=y0+$\frac{p}{2}$=2+$\frac{a}{4}$=3,
解得:a=4,
则抛物线的标准方程为x2=4y,
故选:D.
点评 本题考查抛物线的标准方程,抛物线的焦点弦公式,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.函数$f(x)=\frac{x^3}{3}+\frac{1}{x}$的导数f'(x)=( )
| A. | $\frac{x^2}{3}+\frac{1}{x}$ | B. | ${x^2}-\frac{1}{x^2}$ | C. | $-{x^2}-\frac{1}{x^2}$ | D. | x2+lnx |
10.从1,2,3,4中任取两个数,记作a,b,则两数之和a+b小于5的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.已知f(sin x)=cos 3x,则f(cos 10°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
11.某市5年中的煤气消耗量与使用煤气户数的历史资料如下:
(1)检验是否线性相关;
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
| 年份 | 2006 | 2007 | 2008 | 2009 | 2010 |
| x用户(万户) | 1 | 1.1 | 1.5 | 1.6 | 1.8 |
| y(万立方米) | 6 | 7 | 9 | 11 | 12 |
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
9.积分$\int_1^e{(\frac{1}{x}+2x)dx}$的值为( )
| A. | 1 | B. | e | C. | e+1 | D. | e2 |
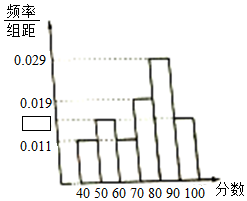 为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.
为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.