题目内容
从分别标有数字1,2,3,4,5,6,7,8,9的9张卡片中任取2张,则两数之和是奇数的概率是 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:列举出所有情况,看取出的两张卡片上的数字之和为奇数的情况数占所有情况数的多少即可.
解答:
解:任取2张的所有情况为(1,2),(1,3),(1,4),(1,5),(1,6),
(1,7),(1,8),(1,9),(2,3),(2,4),(2,5),(2,6),
(2,7),(2,8),(2,9),(3,4),(3,5),(3,6),(3,7),
(3,8),(3,9),(4,5),(4,6),(4,7),(4,8),(4,9),
(5,6),(5,7),(5,8),(5,9),(6,7),(6,8),(6,9),
(7,8),(7,9),(8,9),共36种.其中两数之和是奇数的情况有
(1,2),(1,4),(1,6),(1,8),(2,3),(2,5),(2,7),
(2,9),(3,4),(3,6),(3,8),(4,5),(4,7),(4,9),
(5,6),(5,8),(6,7),(6,9),(7,8),(8,9),共20种情况,
∴两数之和是奇数的概率是
=
.
故答案为:
(1,7),(1,8),(1,9),(2,3),(2,4),(2,5),(2,6),
(2,7),(2,8),(2,9),(3,4),(3,5),(3,6),(3,7),
(3,8),(3,9),(4,5),(4,6),(4,7),(4,8),(4,9),
(5,6),(5,7),(5,8),(5,9),(6,7),(6,8),(6,9),
(7,8),(7,9),(8,9),共36种.其中两数之和是奇数的情况有
(1,2),(1,4),(1,6),(1,8),(2,3),(2,5),(2,7),
(2,9),(3,4),(3,6),(3,8),(4,5),(4,7),(4,9),
(5,6),(5,8),(6,7),(6,9),(7,8),(8,9),共20种情况,
∴两数之和是奇数的概率是
| 20 |
| 36 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:考查用列举的方法解决概率问题;得到取出的两张卡片上的数字之和为奇数的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
相关题目
斜三角形ABC中,命题甲:A=
,命题乙:cosB≠
,则甲是乙的( )
| π |
| 6 |
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设x,y满足
,则z=x-y( )
|
| A、有最小值2,无最大值 |
| B、有最小值-1,无最大值 |
| C、有最大值2,无最小值 |
| D、既无最小值,又无最大值 |
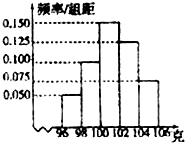 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是