题目内容
17．抛物线y2=4x的焦点为F，P为抛物线上的点，且|PF|=3，则点P到y轴的距离是（ ）| A． | 1 | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
分析 求得抛物线的准线方程，利用抛物线的定义，可得点P到抛物线的焦点F的距离．然后求解即可．
解答 解：抛物线y2=4x的准线方程为x=-1
∵抛物线y2=4x，P为抛物线上的点，且|PF|=3，
∴P到抛物线的准线的距离为3，
∴点P到y轴的距离为2．
故选：B．
点评 本题考查抛物线的性质，考查抛物线的定义，属于基础题．
练习册系列答案
相关题目
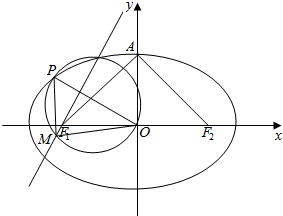如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，点A是椭圆的上顶点，△AF1F2为等腰直角三角形，点P为椭圆任意一点，且|PF1|的最小值为$\sqrt{2}$-1；以OP为直径作圆E，过F1作OP的垂线交圆E于M．