题目内容
已知数列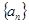 ,
,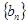 ,
,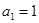 ,
,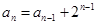 ,
,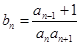 ,
, 为数列
为数列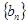 的前
的前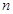 项和,
项和,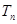 为数列
为数列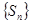 的前
的前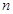 项和.
项和.
(1)求数列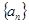 的通项公式;
的通项公式;
(2)求数列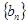 的前
的前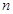 项和
项和 ;
;
(3)求证: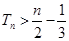 .
.
(1) ;(2)
;(2)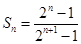 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)解法一是根据数列 递推式的结构选择累加法求数列
递推式的结构选择累加法求数列 的通项公式;解法二是在数列
的通项公式;解法二是在数列 的递推式两边同时除以
的递推式两边同时除以 ,然后利用待定系数法求数列
,然后利用待定系数法求数列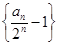 的通项公式,进而求出数列
的通项公式,进而求出数列 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列 的通项公式,然后根据数列
的通项公式,然后根据数列 的通项结构,选择裂项相消法求数列
的通项结构,选择裂项相消法求数列 的前
的前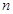 项和
项和 ;(3)对数列
;(3)对数列 中的项利用放缩法
中的项利用放缩法
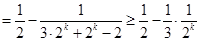 ,然后利用累加法即可证明所要证的不等式.
,然后利用累加法即可证明所要证的不等式.
试题解析:(1)法一:
 ,
,
法二: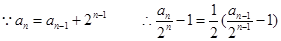
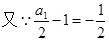


(2)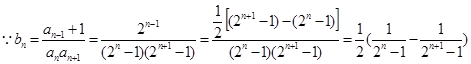
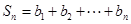
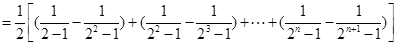

(3)证明: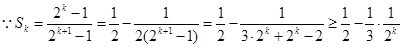 ,
,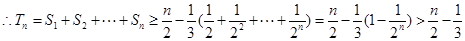 .
.
考点:1.累加法求数列的通项公式;2.待定系数法求数列的通项公式;3.裂项相消法求数列的和;
4.利用放缩法证明数列不等式

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
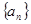 的前n项的和
的前n项的和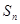 与
与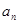 的关系是
的关系是 .
.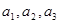 并归纳出数列
并归纳出数列 的前
的前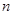 项和
项和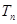 .
.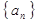 ,满足
,满足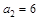 ,
,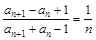
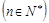 ,
,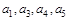 的值;
的值;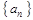 的通项公式
的通项公式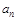 ,并用数学归纳法证明;
,并用数学归纳法证明; ,设
,设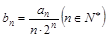 ,记
,记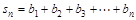 ,求
,求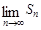 .
.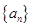 的前n项和为
的前n项和为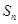 ,且
,且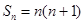 ,数列
,数列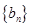 满足
满足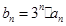 .
.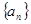 满足
满足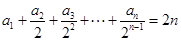 ,
,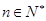 .
.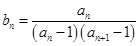 ,求数列
,求数列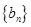 的前
的前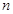 项和
项和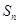 .
.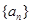 中,
中, 前
前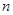 和
和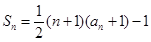
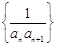 的前
的前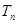 ,是否存在实数
,是否存在实数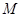 ,使得
,使得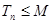 对一切正整数
对一切正整数 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. ,
,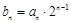 ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn. ,
, 为数列
为数列 的前n项和,则
的前n项和,则 ________.
________.