题目内容
数列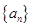 的前n项和为
的前n项和为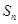 ,且
,且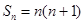 ,数列
,数列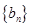 满足
满足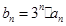 .
.
(1)求数列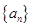 的通项公式,
的通项公式,
(2)求数列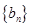 的前n项和.
的前n项和.
(1) ;(2)
;(2) .
.
解析试题分析:(1)通过 求
求 ,然后两式相减得出
,然后两式相减得出 的递推形式,
的递推形式,
 ,不要忘了验证
,不要忘了验证 是否满足
是否满足 ,从而求出
,从而求出 的通项公式; (2)先求出
的通项公式; (2)先求出 ,由形式判定求和用错位相减法,即先列出
,由形式判定求和用错位相减法,即先列出 ,然后再列出
,然后再列出 ,让
,让 ,经过计算,求出
,经过计算,求出 的前n项和
的前n项和 .此题运算量比较大,但思路比较清晰,属于中档题.
.此题运算量比较大,但思路比较清晰,属于中档题.
试题解析:(1)当 ,
,
当 时,
时,
当 时也满足上式,
时也满足上式,
 的通项公式为
的通项公式为
(2)

 ①
① ②
②
①-②得:




考点:1.已知 求
求 ;2.错位相减法求和.
;2.错位相减法求和.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
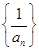 是公差为
是公差为 的等差数列,且
的等差数列,且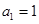 .
.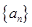 的通项公式;
的通项公式;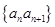 的前
的前 项和为
项和为 .
.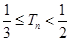 .
.
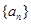 的前项和为
的前项和为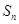 ,且满足
,且满足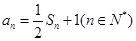 ;
;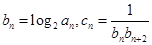 ,且
,且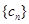 的前n项和为
的前n项和为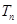 ,求使得
,求使得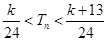 对
对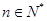 都成立的所有正整数k的值.
都成立的所有正整数k的值.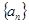 ,
,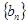 ,
,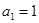 ,
,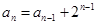 ,
,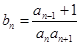 ,
, 为数列
为数列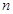 项和,
项和,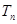 为数列
为数列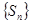 的前
的前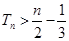 .
.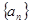 中,
中,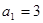 ,其前
,其前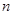 项和为
项和为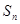 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,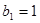 ,公比为
,公比为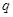 ,且
,且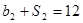 ,
, .
.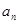 与
与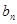 ;
;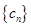 满足
满足 ,求
,求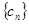 的前
的前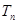 .
. 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 .
. 的通项公式;
的通项公式; ,求证:
,求证: ;
; 的前
的前 .
. 中,
中, ,且满足
,且满足
 .
. 及数列
及数列 求数列
求数列 的前
的前 项和
项和 .
. 的前
的前 项和
项和 ,则数列
,则数列 中数值最小的项是第_项.
中数值最小的项是第_项.