题目内容
设数列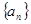 满足
满足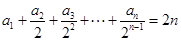 ,
,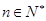 .
.
(1)求数列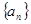 的通项公式;
的通项公式;
(2)设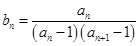 ,求数列
,求数列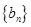 的前
的前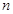 项和
项和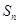 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先令 求出
求出 的值,然后令
的值,然后令 时,在原式中用
时,在原式中用 得到一个新的等式,并将该等式与原等式作差,求出数列
得到一个新的等式,并将该等式与原等式作差,求出数列 在
在 时的通项公式,并对
时的通项公式,并对 的值是否符合上述通项公式进行检验,从而最终确定数列
的值是否符合上述通项公式进行检验,从而最终确定数列 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列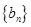 的通项公式
的通项公式 ,并根据数列
,并根据数列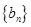 的通项公式结构选择裂项法求和.
的通项公式结构选择裂项法求和.
试题解析:(1)因为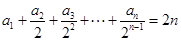 ,
,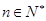 , ①
, ①
所以当 时,
时, .
.
当 时,
时, , ② ,
, ② ,
①-②得, ,所以
,所以 .
.
因为 ,适合上式,所以
,适合上式,所以 ;
;
(2)由(1)得 ,
,
所以 ,
,
所以 .
.
考点:1.定义法求数列的通项公式;2.裂项法求和

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前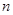 项和为
项和为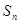 ,且2
,且2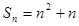 .
.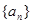 的通项公式;
的通项公式;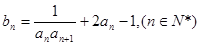 求数列
求数列 的前
的前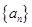 的前
的前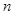 项和为
项和为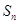 ,且
,且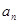 是
是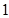 的等差中项,等差数列
的等差中项,等差数列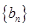 满足
满足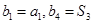
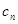 =
=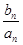 ,求数列
,求数列 的前
的前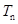 .
.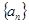 ,
,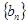 ,
,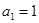 ,
,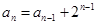 ,
,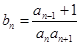 ,
, 为数列
为数列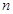 项和,
项和,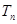 为数列
为数列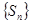 的前
的前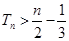 .
.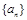 的前n项和为
的前n项和为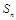 ,且
,且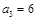 ,
,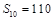 .
.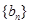 前n项和为
前n项和为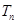 ,且
,且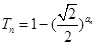 ,令
,令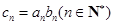 .求数列
.求数列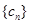 的前n项和
的前n项和 .
. 的前
的前 项和
项和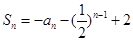 (
( ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,试比较
,试比较 与
与 的大小,并予以证明
的大小,并予以证明 满足
满足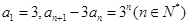 ,数列
,数列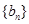 满足
满足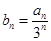 .
. 项和
项和 .
. 满足
满足

 ,求数列
,求数列 的前n项和
的前n项和
 中,
中,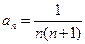 ,前n项和为Sn,则S2009=______________。
,前n项和为Sn,则S2009=______________。