题目内容
设数列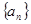 的前n项的和
的前n项的和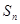 与
与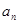 的关系是
的关系是 .
.
(1)求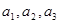 并归纳出数列
并归纳出数列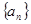 的通项(不需证明);
的通项(不需证明);
(2)求数列 的前
的前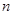 项和
项和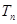 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 ,分别令
,分别令 ,即可求出
,即可求出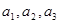 ,根据
,根据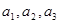 的式子特点即可归纳出数列
的式子特点即可归纳出数列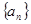 的通项;((2))求数列
的通项;((2))求数列 的前
的前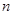 项和
项和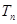 ,由(1) 归纳出数列
,由(1) 归纳出数列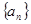 的通项公式,即可得出数列
的通项公式,即可得出数列 的通项公式,利用错位相消法即可得出数列
的通项公式,利用错位相消法即可得出数列 的前
的前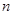 项和
项和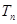 .
.
试题解析:(1): ,
,
所以 .
.
(2)由(1)得 所以
所以 ,由错位相消法得
,由错位相消法得 .
.
考点:归纳推理,数列求和.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 的图象在点
的图象在点 处的切线
处的切线 与直线
与直线 平行,若数
平行,若数 的前
的前 项和为
项和为 ,则
,则 的值为 .
的值为 . 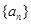 的前
的前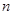 项和为
项和为 ,且
,且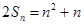 2.
2.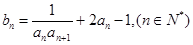 求数列
求数列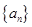 满足:
满足: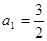 ,
, 
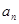 ;
; 满足
满足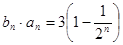 ,求数列
,求数列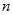 项和.
项和.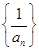 是公差为
是公差为 的等差数列,且
的等差数列,且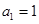 .
.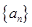 的通项公式;
的通项公式;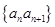 的前
的前 项和为
项和为 .
.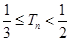 .
. 的前
的前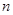 项和为
项和为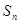 ,且2
,且2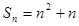 .
.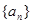 的通项公式;
的通项公式;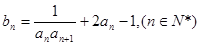 求数列
求数列 的前
的前
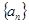 ,
,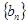 ,
,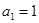 ,
,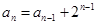 ,
,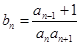 ,
, 为数列
为数列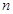 项和,
项和,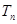 为数列
为数列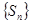 的前
的前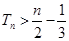 .
. 的前n项和为
的前n项和为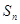 ,
,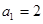 ,当n≥2时,
,当n≥2时, ,
, ,
, 成等差数列. (1)求数列
成等差数列. (1)求数列 的通项公式;
的通项公式; ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.