题目内容
正方体ABCD-A1B1C1D1的棱长为2,MN是它的内切球的一条弦(把球面上任意两点之间的连线段称为球的弦),P为正方体表面上的动点.给出下列命题:
①弦MN的长的取值范围是(0,2
];
②内切球的体积为
;
③直线PM与PN所成角的范围是(0,
];
④当PN是内切球的一条切线时,PN的最大值是
;
⑤线段PN的最大值是
+1.
其中正确的命题是 (把所有正确命题的序号都填上)
①弦MN的长的取值范围是(0,2
| 2 |
②内切球的体积为
| 4π |
| 3 |
③直线PM与PN所成角的范围是(0,
| π |
| 2 |
④当PN是内切球的一条切线时,PN的最大值是
| ||
| 2 |
⑤线段PN的最大值是
| 3 |
其中正确的命题是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:根据MN的最大值为球直径,即|MN|≤2可判断①;
由内切球的直径为2,求出球的体积,可判断②;
根据直线PM与PN所成角最小为0,可判断③;
根据PN是内切球的一条切线时,PN的最大值是
,可判断④;
根据线段PN的最大值是
+1可判断⑤
由内切球的直径为2,求出球的体积,可判断②;
根据直线PM与PN所成角最小为0,可判断③;
根据PN是内切球的一条切线时,PN的最大值是
| 2 |
根据线段PN的最大值是
| 3 |
解答:
解:∵正方体ABCD-A1B1C1D1的棱长为2,MN是它的内切球的一条弦,
故MN的最大值为球直径,即|MN|≤2,
即弦MN的长的取值范围是(0,2],故①错误;
内切球的直径为2,半径为2,体积为
,故②正确;
直线PM与PN所成角的范围是[0,
],故③错误;
当PN是内切球的一条切线时,PN的最大值是
,此时P为正方体的一个顶点,N为内切球与正方体的切点;故④错误;
线段PN的最大值是
+1.此时P为正方体的一个顶点,N为体对角线与球的交点,故⑤正确;
故答案为:②⑤
故MN的最大值为球直径,即|MN|≤2,
即弦MN的长的取值范围是(0,2],故①错误;
内切球的直径为2,半径为2,体积为
| 4π |
| 3 |
直线PM与PN所成角的范围是[0,
| π |
| 2 |
当PN是内切球的一条切线时,PN的最大值是
| 2 |
线段PN的最大值是
| 3 |
故答案为:②⑤
点评:本题以命题的真假判断为载体,考查了正方体的内切球及其相关的距离,夹角,体积等问题,难度中档.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
“a=1”是“行列式
=0”的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
已知l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l⊥α,m?α,则l⊥m |
| B、若l⊥m,m?α,则l⊥α |
| C、若l∥α,m?α,则l∥m |
| D、若l∥α,m∥α,则l∥m |

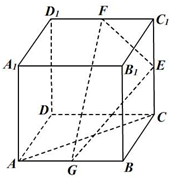 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.