题目内容
8.设实数p在[0,5]上随机地取值,使方程x2+px+1=0有实根的概率为( )| A. | 0.6 | B. | 0.5 | C. | 0.4 | D. | 0.3 |
分析 由题意知方程的判别式大于等于零求出p的范围,再判断出所求的事件符合几何概型,再由几何概型的概率公式求出所求事件的概率.
解答 解:若方程x2+px+1=0有实根,则△=p2-4≥0,
解得,p≥2或 p≤-2;
∵记事件A:“P在[0,5]上随机地取值,关于x的方程x2+px+1=0有实数根”,
由方程x2+px+1=0有实根符合几何概型,
∴P(A)=$\frac{5-2}{5}$=$\frac{3}{5}$=0.6.
故选:A.
点评 本题考查了求几何概型下的随机事件的概率,即求出所有实验结果构成区域的长度和所求事件构成区域的长度,再求比值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.设命题p:$\overrightarrow{a}$=(m,m+1),$\overrightarrow{b}$=(2,m+1),且$\overrightarrow{a}$∥$\overrightarrow{b}$;命题q:关于x的函数y=(m-1)logax(a>0且a≠1)是对数函数,则命题p成立是命题q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不不要条件 |
17.在区间[-1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率( )
| A. | $\frac{1}{48}$ | B. | $\frac{1}{24}$ | C. | $\frac{13}{24}$ | D. | $\frac{11}{24}$ |
18.设全集为实数集R,M={x|x∈R|x≤$\sqrt{5}$},N={1,2,3,4},则∁RM∩N=( )
| A. | {4} | B. | {3,4} | C. | {2,3,4} | D. | {1,2,3,4} |
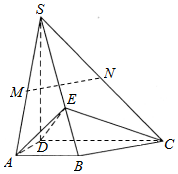 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.