题目内容
3.若圆C:x2+y2-4x+4y+m=与x轴交于A、B两点,且∠ACB=120°,则实数m的值为( )| A. | 24 | B. | -8 | C. | 8 | D. | 4 |
分析 求出圆心C坐标(2,-2),根据垂径定理得出圆C的半径,列出方程解出m.
解答  解:圆C的圆心为C(2,-2),半径r=$\frac{1}{2}$$\sqrt{32-4m}$
解:圆C的圆心为C(2,-2),半径r=$\frac{1}{2}$$\sqrt{32-4m}$
过C作CD⊥AB,垂足为D,连结CA,CB.则CD=2.
∵∠ACB=120°,CA=CB,
∴∠CAD=30°,∴CA=2CD=4,
即$\frac{1}{2}$$\sqrt{32-4m}$=4,解得m=-8.
故选:B.
点评 本题考查了圆的一般方程,直线与圆的位置关系,属于基础题.

练习册系列答案
相关题目
18.已知结合A={y|y=$\sqrt{x^2-2x+5}$,x∈R},函数y=lg(4-x)的定义域为集合B,则A∩B=( )
| A. | (2,4) | B. | [2,4] | C. | [2,4) | D. | [$\sqrt{5}$,4) |
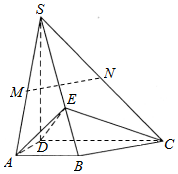 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.