题目内容
 如图所示,一组数排成倒三角形,其中第一行各数依次为1,2,3,…10,从第二行起,每一个数都等于他“肩上”的两个数之和,最后一行只有一个数M,则M=
如图所示,一组数排成倒三角形,其中第一行各数依次为1,2,3,…10,从第二行起,每一个数都等于他“肩上”的两个数之和,最后一行只有一个数M,则M=考点:归纳推理
专题:规律型
分析:从第一行为1,2和1,2,3 和1,2,3,4的两个“小三角形”入手,结合图形归纳得出结果,猜测出M.
解答:
解:若第一行为1,2,则M=3=(2+1)×22-2;
若第一行为1,2,3,则M=8=(3+1)×23-2;
若第一行为1,2,3,4,则M=20=(4+1)×24-2;
…
归纳可得:若第一行为1,2,3,4,…,n,则M=(n+1)×2n-2.
当n=10时,“金字数”M=11×28=2816
故答案为:2816
若第一行为1,2,3,则M=8=(3+1)×23-2;
若第一行为1,2,3,4,则M=20=(4+1)×24-2;
…
归纳可得:若第一行为1,2,3,4,…,n,则M=(n+1)×2n-2.
当n=10时,“金字数”M=11×28=2816
故答案为:2816
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
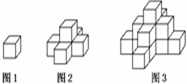 如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是
如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是