题目内容
【题目】数列
中，若对任意
都有
（
为常数）成立，则称为“等差比数列”，下面对“等差比数列” 的判断：①不可能为
；②等差数列一定是等差比数列； ③等比数列一定是等差比数列 ；④通项公式为
（其中
，且
，
）的数列一定是等差比数列，其中正确的判断是（ ）
A. ①③④ B. ②③④ C. ①④ D. ①③
【答案】C
【解析】分析：当
时，则数列成了常数列，则分母也为0，进而推断出
，得出①是正确的，当等差数列和等比数列为常数列时不满足题设条件，排除②③，把④的通项公式代入题设中，满足条件，进而推断④是正确的.
详解：对于①中，若时，则分母也为0，所以，得出①是正确；
当当等差数列和等比数列为常数列时不满足题设条件，排除②③，
对于④中，把
代入
结果为
（常数），所以是正确的，
综上所述，正确的命题为①④，故选C.
练习册系列答案
相关题目
【题目】某校为调查高一、高二学生周日在家学习用时情况，随机抽取了高一、高二各
人，对他们的学习时间进行了统计，分别得到了高一学生学习时间（单位：小时）的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表（学习时间均在区间
内）：
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图：
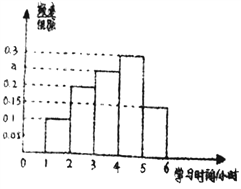
（1）求高二学生学习时间的频率分布直方图中的
值，并根据此频率分布直方图估计该校高二学生学习时间的中位数；
（2）利用分层抽样的方法，从高一学生学习时间在
，
的两组里随机抽取
人，再从这人中随机抽取
人，求学习时间在这一组中至少有
人被抽中的概率.
