题目内容
【题目】已知圆 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作圆
作圆 ![]() 的切线
的切线 ![]() ,切点为
,切点为 ![]() .
.
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求切线
,求切线 ![]() 的方程;
的方程;
(2)求四边形 ![]() 面积的最小值;
面积的最小值;
(3)求证:经过 ![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
【答案】
(1)解:①当切线斜率不存在时,切线方程为 ![]() ;
;
②当切线斜率存在时,设切线方程为 ![]() ,
,
因为直线和圆相切,所以圆心 ![]() 到切线的距离
到切线的距离 ![]() ,解得
,解得 ![]() ,
,
所以切线方程为 ![]() ,即
,即 ![]() .
.
故答案为:所求切线方程为 ![]() 或
或 ![]()
(2)解:四边形 ![]() 的面积
的面积 ![]() ,
,
所以当 ![]() 最小时,四边形
最小时,四边形 ![]() 的面积
的面积 ![]() 最小.
最小.
又 ![]() 的最小值是圆心
的最小值是圆心 ![]() 到直线
到直线 ![]() 的距离,
的距离,
即 ![]() .
.
故答案为:四边形 ![]() 的面积最小值是
的面积最小值是 ![]() .
.
(3)证明:过 ![]() 三点的圆即以
三点的圆即以 ![]() 为直径的圆,
为直径的圆,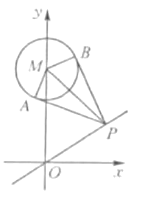
设点 ![]() ,则圆心坐标是
,则圆心坐标是 ![]() ,
,
以 ![]() 为直径的圆的方程是
为直径的圆的方程是 ![]()
![]() ,
,
化简,得 ![]() ,
,
即 ![]() .(*)
.(*)
令 ![]() ,解得
,解得 ![]() 或
或 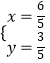 .
.
由于不论 ![]() 为何值,点
为何值,点 ![]() 、
、 ![]() 的坐标都适合方程(*),所以经过
的坐标都适合方程(*),所以经过 ![]() 三点的圆必过定点.
三点的圆必过定点.
故答案为:定点坐标是 ![]() 和
和 ![]() .
.
【解析】(1)利用圆心到直线的距离相等求切线方程,注意直线存在的情况;
(2)先将四边形的面积表示为|PM|的函数式,通过求|PM|的最值得到四边形面积的最值;
(3)将圆的方程表示为圆系方程的形式,求出圆过定点的坐标.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: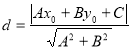 .
.

练习册系列答案
相关题目