Question

【题目】已知动圆 过定点 ，且在定圆 的内部与其相内切.
（1）求动圆圆心 的轨迹方程 ；
（2）直线 与 交于 两点，与圆 交于 两点，求 的值.

Answer 1

【答案】
（1）解：如图所示，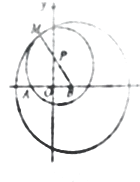

设动圆 和定圆 内切于点 .动点 到两定点，即定点 和定圆圆心 距离之和恰好等于定圆半径，
即 ，
故答案为:点 的轨迹 是以 为两焦点，半长轴为2，半短轴长为 的椭圆： .
（2）解：将 代入 得， ，
所以 ，又由垂径定理得，
.
故答案为: .
【解析】(1)由圆的切线的性质结合椭圆的定义求轨迹方程;
(2)将直线方程与椭圆方程联立,消去y得关于x的一元二次方程,由弦长公式求|CD|和|GH|,得结果.