题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,函数g(x)=f[f(x)]-$\frac{1}{2}$的三个零点为x1,x2,x3,且x1<x2<x3,则( )| A. | x2+x3=$\frac{3}{4}$ | B. | x2+x3=1 | C. | x1+x2=$\frac{1}{4}$ | D. | x1+x2=-$\frac{1}{4}$ |
分析 令f[f(x)]-$\frac{1}{2}$=0,从而可得f(x)=$\frac{\sqrt{2}}{2}$或f(x)=-1,再讨论分别求解,从而确定三个零点,从而解得.
解答 解:令f[f(x)]-$\frac{1}{2}$=0,
即1+log2f(x)-$\frac{1}{2}$=0或2f(x)-$\frac{1}{2}$=0,
解得,f(x)=$\frac{\sqrt{2}}{2}$或f(x)=-1,
若f(x)=$\frac{\sqrt{2}}{2}$,
则1+log2x=$\frac{\sqrt{2}}{2}$或2x=$\frac{\sqrt{2}}{2}$,
则log2x=$\frac{\sqrt{2}}{2}$-1或x=-$\frac{1}{2}$,
若f(x)=-1,
则1+log2x=-1,
故x=$\frac{1}{4}$,
故x1=-$\frac{1}{2}$,x2=$\frac{1}{4}$,log2x3=$\frac{\sqrt{2}}{2}$-1;
故选:D.
点评 本题考查了函数的零点与方程的根的关系应用及复合函数的性质的应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
15.已知集合A={x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是( )
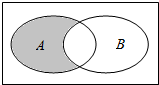

| A. | {x|2<x<3} | B. | {x|-1<x≤0} | C. | {x|0≤x<6} | D. | {x|x<-1} |