题目内容
20.函数$f(x)=\frac{sinx}{|sinx|}+\frac{2cosx}{|cosx|}+\frac{3tanx}{|tanx|}$的值域为A,则集合A的子集个数为( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
分析 分类讨论,确定A的元素的个数,即可求出集合A的子集个数.
解答 解:由题意,x在第一象限,f(x)=1+2+3=6;
x在第二象限,f(x)=1-2-3=-4;
x在第三象限,f(x)=-1-2+3=0;
x在第四象限,f(x)=-1+2-3=-2,
∴A={-4,-2,0,6},
∴集合M的子集个数为24=16,
故选:C.
点评 本题考查集合M的子集个数,考查分类讨论的数学思想,比较基础.

练习册系列答案
相关题目
10.已知等比数列{an}的公比q=2,a4=8,Sn为{an}的前n项和,设a=a20.3,b=0.3${\;}^{{a}_{3}}$,c=logan(Sn+$\frac{1}{{S}_{n}}$),则a,b,c大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
15.设函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0)的最小正周期为π,则“f(-x)=f(x)”是“φ=$\frac{π}{4}$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.一个正三棱柱的正视图如图所示,已知它的体积为3,则该正三棱柱的高为( )
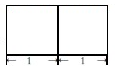

| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
10.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F1,左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+$\sqrt{{a}^{2}+{b}^{2}}$,则该双曲线的离心率取值范围是( )
| A. | (1-$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (1,2$\sqrt{2}$) | D. | (2$\sqrt{2}$,+∞) |
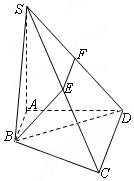 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.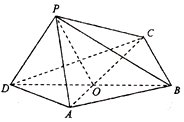 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.