题目内容
数列{an}中，Sn为其前n项和，Sn=n2-2n+3，则an= ．
【答案】分析：根据Sn，表示出数列{an}的前n-1项和Sn-1，两式相减即可求出此数列的通项公式，然后把n=1代入看是否满足，从而可求出的an．
解答：解：a1=S1=1-2+3=2，
当n≥2时an=Sn-Sn-1=（n2-2n+3）-[（n-1）2-2（n-1）+3]=2n-3，
当n=1时，2n-3=-1≠a1，
∴an=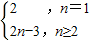
故答案为：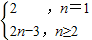
点评：本题主要考查了等差数列的通项公式，灵活运用an=Sn-Sn-1求出数列的通项公式，属于基础题．
解答：解：a1=S1=1-2+3=2，
当n≥2时an=Sn-Sn-1=（n2-2n+3）-[（n-1）2-2（n-1）+3]=2n-3，
当n=1时，2n-3=-1≠a1，
∴an=
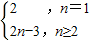
故答案为：
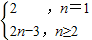
点评：本题主要考查了等差数列的通项公式，灵活运用an=Sn-Sn-1求出数列的通项公式，属于基础题．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
在数列{an}中，Sn为其前n项之和，且Sn=2n-1，则a12+a22+a32+…+an2等于：
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|