题目内容
已知公差不为0的等差数列{an}的前n项和为Sn，且a5=3a2，若S6=λa7，则λ= ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用a5=3a2，可得d=2a1，再利用S6=λa7，求出λ的值．
解答：
解：设公差为d，则a1+4d=3（a1+d），
∴d=2a1，
∵S6=λa7，
∴6a1+15d=λ（a1+6d），
∴6a1+30a1=λ（a1+12a1），
∴λ=
．
故答案为：
．
∴d=2a1，
∵S6=λa7，
∴6a1+15d=λ（a1+6d），
∴6a1+30a1=λ（a1+12a1），
∴λ=
| 36 |
| 13 |
故答案为：
| 36 |
| 13 |
点评：本题考查等差数列的通项与求和，考查学生的计算能力，比较基础．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
已知原命题“若两个三角形全等，则这两个三角形面积相等”，那么它的逆命题、否命题、逆否命题中，真命题的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
给出的四个程序框图，其中满足WHILE语句结构的是（ ）
| A、①② | B、②③ | C、②④ | D、③④ |
适合方程2z-|z|-i=0的复数z是（ ）
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、±
|
已知全集U={2011，2012，2013，2014，2015}，M={2011，2012，2013}，则∁UM=（ ）
| A、{2014} |
| B、{2014，2015} |
| C、{2011，2012，2013} |
| D、{2011，2012，2013，2014，2015} |
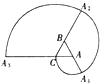如图，一条螺旋线是用以下方法画成的：△ABC是边长为1的正三角形，曲线CA1，A1A2，A2A3是分别以A、B、C为圆心，AC、BA1、CA2为半径画的圆弧，曲线CA1A2A3称为螺旋线的第一圈，然后又以A为圆心，AA3为半径画圆弧…这样画到第n圈，则所得螺旋线的长度ln为（ ）| A、（3n2+n）π | ||
| B、（3n2-n+1）π | ||
C、
| ||
D、
|