题目内容
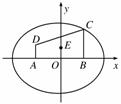如图，在直角坐标系xOy中有一直角梯形ABCD，AB的中点为O，AD⊥AB，AD∥BC，AB＝4，BC＝3，AD＝1，以A，B为焦点的椭圆经
过点C.
(1)求椭圆的标准方程；
(2)若点E(0,1)，问是否存在直线l与椭圆交于M，N两点且|ME|＝|NE|，若存在，求出直线l斜率的取值范围；若不存在，请说明理由．
解：(1)连接AC，依题意设椭圆的标准方程为：
＋
＝1(a＞b＞0)，
在Rt△ABC中，AB＝4，BC＝3，
∴AC＝5.
∴CA＋CB＝5＋3＝2a，a＝4.
又2c＝4，∴c＝2，
从而b＝ 
＝2
，
∴椭圆的标准方程为
＝1.
(2)由题意知，当l与x轴垂直时，不满足|ME|＝|NE|，
当l与x轴平行时，|ME|＝|NE|显然成立，此时k＝0.
设直线l的方程为y＝kx＋m(k≠0)，
∴16k2＋12＞m2.①
令M(x1，y1)，N(x2，y2)，MN的中点为F(x0，y0)，
综上所述，存在满足条件的直线l，且其斜率k的取值范围为(－
，)．
练习册系列答案
相关题目
（2009•杭州二模）如图，在直角坐标系xOy中，锐角△ABC内接于圆x2+y2=1．已知BC平行于x轴，AB所在直线方程为y=kx+m（k＞0），记角A，B，C所对的边分别是a，b，c．
如图，在直角坐标系中，中心在原点，焦点在X轴上的椭圆G的离心率为
（2013•石景山区二模）如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且
如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且
如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：