题目内容
已知函数f(x)=
,函数g(x)=acos
-2a+
(a<0),若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
|
| πx |
| 2 |
| 1 |
| 2 |
考点:函数的值域
专题:导数的综合应用,三角函数的图像与性质
分析:根据f(x)的解析式求出其值域,再求出g(x)在x∈[0,1]上的值域,由存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明g(x)的最值中至少一个在f(x)的值域内,从而求出a的取值范围.
解答:
解:∵f(x)=
,
∴f′(x)=
=
,
当x∈(
,]时,f′(x)>0,函数f(x)在(
,1]上为增函数,∴f(x)∈(
,1];
当x∈[0,
]时,函数f(x)为减函数,∴f(x)∈[0,
];
∴在[0,1]上f(x)∈[0,1];
又g(x)=acos
-2a+
中,
当x∈[0,1]时,cos
∈[0,1],
∴g(x)∈[-2a+
,-a+
];
若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,
说明函数g(x)的最大值与最小值中至少有一个在[0,1]中,
∴0≤-2a+
≤1或0≤-a+
≤1,
解得-
≤a≤
,或-
≤a≤
,
又a<0,
∴实数a的取值范围是{a|-
≤a<0}.
故答案为:{a|-
≤a<0}.
| 2x3 |
| x+1 |
∴f′(x)=
| 6x2(x+1)-2x3 |
| (x+1)2 |
| 4x3+6x2 |
| (x+1)2 |
当x∈(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
当x∈[0,
| 1 |
| 2 |
| 1 |
| 6 |
∴在[0,1]上f(x)∈[0,1];
又g(x)=acos
| πx |
| 2 |
| 1 |
| 2 |
当x∈[0,1]时,cos
| πx |
| 2 |
∴g(x)∈[-2a+
| 1 |
| 2 |
| 1 |
| 2 |
若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,
说明函数g(x)的最大值与最小值中至少有一个在[0,1]中,
∴0≤-2a+
| 1 |
| 2 |
| 1 |
| 2 |
解得-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
又a<0,
∴实数a的取值范围是{a|-
| 1 |
| 2 |
故答案为:{a|-
| 1 |
| 2 |
点评:本题考查了函数的零点以及数学转化思想,解题时应把函数零点的研究转化为元素与集合之间的关系问题来解答,是较难的题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
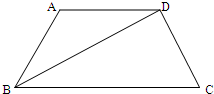 如图,在四边形ABCD中,
如图,在四边形ABCD中,