Question

【题目】已知数列，，为数列的前项和，向量，，

．

（1）若，求数列通项公式；

（2）若，．

①证明：数列为等差数列；

②设数列满足，问是否存在正整数，，且，，使得、、成等比数列，若存在，求出、的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）①见解析；②存在，符合题意.

【解析】分析：（1）利用两个向量平行的坐标关系得到，进而求解数列的通项公式；

（2）①由，则，又由，两式相减即可得到数列的递推公式，进而得到数列的首项和公差，即可作出证明.

②中由①得到数列的通项公式，根据的范围，讨论可能的取值，即可得到结论.

详解：（1）因为，，

得：，当，则①

当时，，即

又②

②－①得：，

即，所以，又，

所以是首项为2，公比为2的等比数列

所以

（2）①证明：因为，则③

当时，，即

又④

④－③得：

即：⑤

又⑥

⑥－⑤得：

即，所以数列为等差数列．

②又，，

所以数列是首项为，公差为的等差数列．

，所以，

假设存在正整数，，且，，使得、、成等比数列，

即，

可得：

整理得：，即，

由，得，

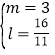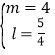一一代入检验或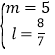或或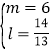或或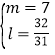或或

由，为正整数，，且，，所以存在，符合题意