题目内容
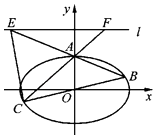
【题目】已知双曲线 
，以原点为圆心，双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于 
四点，四边形 
的面积为 
，则双曲线的离心率为（ ）
A.
B.2
C.
D.4
【答案】B
【解析】由题意可得，双曲线的渐近线方程为 
，圆的方程为 
，
联立直线方程与圆的方程可得： 
，
据此计算可得： 
，
结合图形的对称性可得 
的坐标分别为： 
，
结合面积公式和四边形的面积为： 
，
整理可得： 
，则 
，
双曲线的离心率为： 
.
故答案为：B.
根据题目中所给的条件的特点，先求出以原点为圆心，双曲线的实半轴长为半径长的圆的方程，从而得到双曲线的两条渐近线方程，最后利用四边形ABCD的面积为ab，求出A的坐标，代入圆的方程，结合离心率公式，即可得出结论．
练习册系列答案
相关题目
