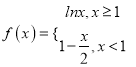题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)设![]() ,求函数
,求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析: ![]() 根据题意得当
根据题意得当![]() 时,
时, ![]() 代入得
代入得![]() 由切线方程知,
由切线方程知, ![]() 联立解得
联立解得![]() ,
, ![]() 的值(2)表示
的值(2)表示![]() ,求导然后分类讨论
,求导然后分类讨论
当![]() 时和当
时和当![]() 时两种情况
时两种情况
解析:(1)由切线方程知,当![]() 时,
时, ![]() ,∴
,∴![]()
∵![]() ,∴由切线方程知,
,∴由切线方程知, ![]()
∴![]()
(2)由(1)知, ![]() ∴
∴![]() ,
, ![]()
当![]() 时,当
时,当![]() 时,
时, ![]() ,故
,故![]() 单调递减
单调递减
∴![]() 在
在![]() 上的最大值为
上的最大值为![]()
②当![]() 时
时
∵![]() ,
, ![]() ,∴存在
,∴存在![]() ,使
,使![]()
当![]() 时,
时, ![]() ,故
,故![]() 单调递减
单调递减
当![]() 时,
时, ![]() ,故
,故![]() 单调递增∴
单调递增∴![]() 在
在![]() 上的最大值为
上的最大值为![]() 或
或![]()
又![]() ,
, ![]() ,∴当
,∴当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]()
当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]()
当![]() 时,当
时,当![]() 时,
时, ![]() ,故
,故![]() 单调递增
单调递增
∴![]() 在
在![]() 上的最大值为
上的最大值为![]()
综上所述,当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]()
当![]() 时,
时, ![]() 在
在![]() 上的最大值为
上的最大值为![]()

练习册系列答案
相关题目