题目内容
已知非零复数z1,z2满足|z1|=a,|z2|=b,|z1+z2|=c(a、b、c均大于零),问是否根据上述条件求出 ?请说明理由.
?请说明理由.
 ?请说明理由.
?请说明理由. 解此方程a2( )2+(a2+b2–c2)(
)2+(a2+b2–c2)( )+b2=0即得
)+b2=0即得 的值
的值
 )2+(a2+b2–c2)(
)2+(a2+b2–c2)( )+b2=0即得
)+b2=0即得 的值
的值∵|z1+z2|2=(z1+z2)( +
+ )=|z1|2+|z2|2+(z1
)=|z1|2+|z2|2+(z1 +
+ z2)
z2)
∴c2=a2+b2+(z1 +
+ z2)
z2)
即:z1 +
+ z2=c2–a2–b2
z2=c2–a2–b2
∵z1≠0,z2≠0,∴z1 +
+ ·z2=
·z2= =|z2|2(
=|z2|2( )+|z1|2(
)+|z1|2( )
)
即有:b2( )+a2(
)+a2( )=z1z2+z1z2
)=z1z2+z1z2
∴b2( )+a2(
)+a2( )=c2–a2–b2
)=c2–a2–b2
∴a2( )2+(a2+b2–c2)(
)2+(a2+b2–c2)( )+b2=0
)+b2=0
这是关于 的一元二次方程,解此方程即得
的一元二次方程,解此方程即得 的值.
的值.
 +
+ )=|z1|2+|z2|2+(z1
)=|z1|2+|z2|2+(z1 +
+ z2)
z2)∴c2=a2+b2+(z1
 +
+ z2)
z2)即:z1
 +
+ z2=c2–a2–b2
z2=c2–a2–b2∵z1≠0,z2≠0,∴z1
 +
+ ·z2=
·z2= =|z2|2(
=|z2|2( )+|z1|2(
)+|z1|2( )
)即有:b2(
 )+a2(
)+a2( )=z1z2+z1z2
)=z1z2+z1z2∴b2(
 )+a2(
)+a2( )=c2–a2–b2
)=c2–a2–b2∴a2(
 )2+(a2+b2–c2)(
)2+(a2+b2–c2)( )+b2=0
)+b2=0这是关于
 的一元二次方程,解此方程即得
的一元二次方程,解此方程即得 的值.
的值.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 )n+(
)n+( )n,n∈N,如果A
)n,n∈N,如果A {f(n)},则满足条件的集合A有
{f(n)},则满足条件的集合A有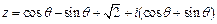 ,当
,当 为何值时,
为何值时,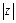 取得最大值,并求此最大值.
取得最大值,并求此最大值.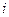 是虚数单位,
是虚数单位,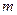 和
和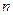 都是实数,且
都是实数,且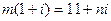 ,则
,则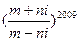 等于( )
等于( )



 ,其中
,其中 、
、 ,
, 是虚数单位,则
是虚数单位,则 等于( )
等于( ) 

 的实部与虚部相等,则实数b的值为___________
的实部与虚部相等,则实数b的值为___________ .
. ( )
( )

