题目内容
若椭圆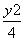
＋
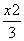＝1的两个焦点F1，F2，M是椭圆上一点，且|MF1|－|MF2|＝1，则△MF1F2是（ ）
A．钝角三角形 B．直角三角形 C．锐角三角形 D．等边三角形
B
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案题目内容
若椭圆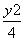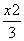＋＝1的两个焦点F1，F2，M是椭圆上一点，且|MF1|－|MF2|＝1，则△MF1F2是（ ）
A．钝角三角形 B．直角三角形 C．锐角三角形 D．等边三角形
B
云南师大附小一线名师提优作业系列答案冲刺100分单元优化练考卷系列答案
，
，在
中，正数的个数是（ ）
，
，其中
.
时，求
的值；
时，求
的最大值.
,则“
且
”是“点
在直线
上”的 （ ）
为直角梯形，
，
平面
，
.
与
所成角的余弦值；
与平面
所成角的正弦值；
的余弦值.
为平面内两定点,过该平面内动点
作直线
的垂线,垂足为
.若
,其中
为常数,则动点
:对任意实数
，不等式
恒成立；命题
:方程
表示焦点在
的取值范围；
”为真命题，且“
”为假命题，求实数
满足
,且在
时, 
,
，
图象交点的个数是 .
可能取的值为1，2，3，4；
（
1，2，3，4）.
.