题目内容
已知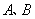 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点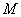 作直线
作直线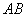 的垂线,垂足为
的垂线,垂足为 .若
.若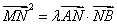 ,其中
,其中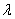 为常数,则动点
为常数,则动点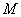 的轨迹不可能是( )
的轨迹不可能是( )
A.圆 B.椭圆 C.抛物线 D.双曲线
C

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
题目内容
已知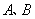 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点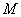 作直线
作直线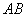 的垂线,垂足为
的垂线,垂足为 .若
.若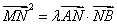 ,其中
,其中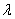 为常数,则动点
为常数,则动点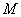 的轨迹不可能是( )
的轨迹不可能是( )
A.圆 B.椭圆 C.抛物线 D.双曲线
C

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案