题目内容
12.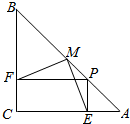 设点M是等腰直角三角形ABC的斜边BA的中点,P是直线BA上任意一点,PE⊥AC于E,PF⊥BC于F,求证:
设点M是等腰直角三角形ABC的斜边BA的中点,P是直线BA上任意一点,PE⊥AC于E,PF⊥BC于F,求证:(1)ME=MF;
(2)ME⊥MF.
分析 (1)以等腰直角三角形的直角顶点C为坐标原点O,以OA为单位长,以直线OA.OB分别为x轴.y轴建立平面直角坐标系,由此能证明ME=MF.
(2)分别求出ME2+MF2=${{x}_{0}}^{2}+{{y}_{0}}^{2}$,$E{F^2}={x_0}^2+{y_0}^2$,由此能证明ME⊥MF.
解答 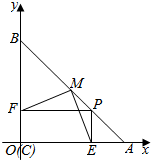 证明:(1)如图,以等腰直角三角形的直角顶点C为坐标原点O,
证明:(1)如图,以等腰直角三角形的直角顶点C为坐标原点O,
以OA为单位长,以直线OA.OB分别为x轴.y轴建立平面直角坐标系,
则A(1,0),B(0,1),$M(\frac{1}{2},\frac{1}{2})$…(2分)
设P(x0,y0),则有x0+y0=1,
∵PE⊥OA,PF⊥OB,∴E(x0,0),F(0,y0),$ME=\sqrt{{{({x_0}-\frac{1}{2})}^2}+\frac{1}{4}}$,$MF=\sqrt{\frac{1}{4}+{{(\frac{1}{2}-{y_0})}^2}}$,
∵${x}_{0}-\frac{1}{2}=\frac{1}{2}-{y}_{0}$,∴ME=MF.…(7分)
(2)∵ME2+MF2=(${x}_{0}-\frac{1}{2}$)2+$\frac{1}{4}$+$\frac{1}{4}$+($\frac{1}{2}$-y0)2=${{x}_{0}}^{2}+{{y}_{0}}^{2}$,
$E{F^2}={x_0}^2+{y_0}^2$,
∴ME2+MF2=EF2,∴ME⊥MF.…(12分)
点评 本题考查线段长相等和两直线垂直的证明,是基础题,解题时要认真审题,注意合理建立平面直角坐标系.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.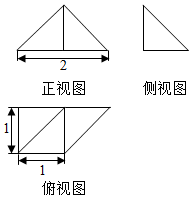 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5+\sqrt{3}}{2}$ | D. | $\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$ |
17.已知某几何体的三视图如图,其中主视图中半圆的直径为2,则该几何体的表面积为( )

| A. | 46 | B. | 52-π | C. | 52+3π | D. | 46+2π |
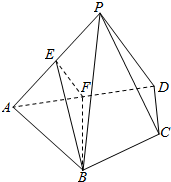 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.