题目内容
20.在△ABC中,角A,B,C的对边分别为a,b,c,若sinA+sinC=$\sqrt{2}$sinB,则△ABC中最大角的度数等于( )| A. | 90° | B. | 75° | C. | 135° | D. | 105° |
分析 由已知利用正弦定理可得:a+c=$\sqrt{2}$b,两边平方可得:a2+c2-b2=b2-2ac,又利用基本不等式可求b2≥2ac,可求B为最大角,进而利用余弦定理可求cosB≥0,根据余弦函数的图象可求B的最大值.
解答 解:∵sinA+sinC=$\sqrt{2}$sinB,
∴由正弦定理可得:a+c=$\sqrt{2}$b,
∴两边平方可得:a2+c2+2ac=2b2,可得:a2+c2-b2=b2-2ac,
∵a2+c2=2b2-2ac≥2ac,可得:b2≥2ac,当且仅当a=c时等号成立,
∴B为最大角,由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{b}^{2}-2ac}{2ac}$≥$\frac{2ac-2ac}{2ac}$=0,
当且仅当a=c时等号成立,
由B∈(0°,180°),
可求Bmax=90°.
故选:A.
点评 本题主要考查了正弦定理,基本不等式,余弦定理,余弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
15.下列各图中,表示以x为自变量的奇函数的图象是( )
| A. | 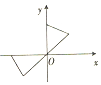 | B. | 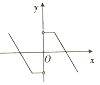 | C. |  | D. |  |
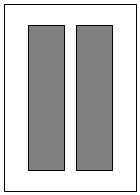 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm