题目内容
15.如图,在平面直角坐标系xoy中,将直线$y=\frac{x}{2}$与直线x=1及x轴所围成的图形绕x轴旋转一周得到一个圆锥,圆锥的体积$V=\int_0^1{π{{({\frac{x}{2}})}^2}dx=\frac{π}{12}{x^3}|_0^1}=\frac{π}{12}$,以此类比:将曲线y=x2(x≥0)与直线y=2及y轴所围成( )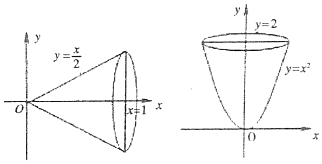
| A. | π | B. | 2π | C. | 3π | D. | 4π |
分析 根据类比推理,结合定积分的应用,即可求出旋转体的体积.
解答 解:根据类比推理得体积V=${∫}_{0}^{2}$π($\sqrt{y}$)2dy=${∫}_{0}^{2}$πydy=$\frac{1}{2}$πy2|${\;}_{0}^{2}$=2π,
故选:B
点评 本题主要考查旋转体的体积的计算,根据类比推理是解决本题的关键.

练习册系列答案
相关题目
5.设△ABC的内角A,B,C所对的边分别是a,b,c,设向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(sinB,sinA),若$\overrightarrow{m}$∥$\overrightarrow{n}$,则△ABC为( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 无法确定 |
6.函数f(x)的导函数f'(x),满足关系式f(x)=x2+2xf'(2)-lnx,则f'(2)的值为( )
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
5.复数1-$\sqrt{3}$i的虚部为( )
| A. | $\sqrt{3}$i | B. | 1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
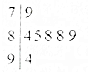 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )