圆C:x2+y2-2x-2y+1=0的圆心坐标是(1.1).直线l:x-y=0与圆C相交于A.B两点.则|AB|=2．题目和参考答案——青夏教育精英家教网——

题目内容

4．圆C：x²+y²-2x-2y+1=0的圆心坐标是（1，1），直线l：x-y=0与圆C相交于A，B两点，则|AB|=2．

分析本题可以将圆的普通方程化成为标准方程，得到圆心坐标和半径长，得到本题结论．

解答解：∵圆C：x²+y²-2x-2y+1=0，
∴（x-1）²+（y-1）²=1，
∴圆C：x²+y²-2x-2y+1=0的圆心坐标和半径分别为：（1，1），1．
圆心在直线l：x-y=0，∴|AB|=2，
故答案为：（1，1），2．

点评本题考查了圆的普通方程和标准方程的互化，本题难度不大，属于基础题．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

14．对于定义域为R的函数g（x），若函数sin[g（x）]是奇函数，则称g（x）为正弦奇函数．已知f（x）是单调递增的正弦奇函数，其值域为R，f（0）=0．
（1）已知g（x）是正弦奇函数，证明：“u₀为方程sin[g（x）]=1的解”的充要条件是“-u₀为方程sin[g（x）]=-1的解”；
（2）若f（a）=$\frac{π}{2}$，f（b）=-$\frac{π}{2}$，求a+b的值；
（3）证明：f（x）是奇函数．

15．如图，在平面直角坐标系xoy中，将直线$y=\frac{x}{2}$与直线x=1及x轴所围成的图形绕x轴旋转一周得到一个圆锥，圆锥的体积$V=\int_0^1{π{{（{\frac{x}{2}}）}^2}dx=\frac{π}{12}{x^3}|_0^1}=\frac{π}{12}$，以此类比：将曲线y=x²（x≥0）与直线y=2及y轴所围成（　　）

12．某校为了解学生的学习情况，采用分层抽样的方法从高一150人、高二120人、高三180人中抽取50人进行问卷调查，则高三抽取的人数是20．

19．函数f（x）定义在（-∞，+∞）上．则“曲线：y=f（x）过原点”是“f（x）为奇函数”的（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分也不必要条件

9．在测试中，客观题难度的计算公式为P_i=$\frac{{R}_{i}}{N}$，其中P_i为第i题的难度，R_i为答对该题的人数，N为参加测试的总人数．
现对某校髙三年级120名学生进行一次测试，共5道客观题．测试前根据对学生的了解，预估了每道题的难度，如表所示：

题号	1	2	3	4	5
考前预估难度P_i	0.9	0.8	0.7	0.6	0.4

测试后，从中随机抽取了10名学生，将他们编号后统计各题的作答情况，如表所示（“√”表示答对，“×”表示答错）：

题号学生编号	1	2	3	4	5
1	×	√	√	√	√
2	√	√	√	√	×
3	√	√	√	√	×
4	√	√	√	×	×
5	√	√	√	√	√
6	√	×	×	√	×
7	×	√	√	√	×
8	√	×	×	×	×
9	√	√	√	×	×
10	√	√	√	√	×

（I）根据题中数据，将抽样的10名学生每道题实测的答对人数及相应的实测难度填入表，并估计这120名学生中第5题的实测答对人数；

题号	1	2	3	4	5
实测答对人数
实测难度

（Ⅱ）从编号为1到5的5人中随机抽取2人，求恰好有1人答对第5题的概率；
（Ⅲ）定义统计量S=$\frac{1}{n}$[（P′₁-P₁）²+（P′₂-P₂）²+…+（P′_n-P_n）²]，其中P′_i为第i题的实测难度，P_i为第i题的预估难度（i=l，2，…，n），规定：若S＜0.05，则称该次测试的难度预估合理，否则为不合理．判断本次测试的难度预估是否合理．

16．下列命题中，正确的是（　　）

	A．	命题“?x∈（0，$\frac{π}{4}$），sinx＞cosx”的否定是“?x₀∈（0，$\frac{π}{4}$），sinx＜cosx”
	B．	函数y=sinx+cosx的最大值是$\sqrt{2}$
	C．	已知a，b为实数，则a+b=0的充要条件是$\frac{a}{b}$=-1
	D．	函数y=2cos²（x-$\frac{π}{4}$）-1既不是奇函数，也不是偶函数

13．设正实数a，b满足a+b=1，则（　　）

$\frac{1}{a}+\frac{1}{b}$有最大值4

$\sqrt{ab}$有最小值 $\frac{1}{2}$

$\sqrt{a}+\sqrt{b}$有最大值$\sqrt{2}$

a²+b²有最小值$\frac{{\sqrt{2}}}{2}$

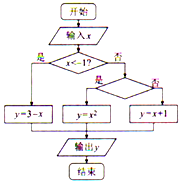已知分段函数y=$\left\{\begin{array}{l}{3-x，x＜-1}\\{{x}^{2}，-1≤x≤1}\\{x+1，x＞1}\end{array}\right.$，若执行如图所示的程序框图，则框图中的条件应该填写（　　）