题目内容
若直线l沿x轴向右平移3个单位,再沿y轴向上平移2个单位,回到原来位置,则直线l的斜率为 .
考点:直线的斜率
专题:直线与圆
分析:由直线的平移变换可得平移后的直线方程,比较系数可得.
解答:
解:设直线的斜率为k,且方程为y=kx+b,①
∴直线l沿x轴向右平移3个单位后得到的方程为y=k(x-3)+b,
再沿y轴向上平移2个单位后得到的方程为y=k(x-3)+b+2,②
∵回到原来位置,∴方程①②应为同一个,
比较系数可得-3k+b+2=b,解得k=
故答案为:
.
∴直线l沿x轴向右平移3个单位后得到的方程为y=k(x-3)+b,
再沿y轴向上平移2个单位后得到的方程为y=k(x-3)+b+2,②
∵回到原来位置,∴方程①②应为同一个,
比较系数可得-3k+b+2=b,解得k=
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查直线的斜率,涉及直线的平移变换,属基础题.

练习册系列答案
相关题目
已知a是实数,i是虚数单位,
是纯虚数,则a的值为( )
| 1+ai |
| 1-i |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
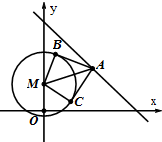 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.