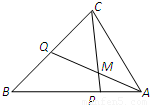
题目内容
 在△ABC中,点P是AB上一点,且
在△ABC中,点P是AB上一点,且 ,Q是BC中点,AQ与CP交点为M,又
,Q是BC中点,AQ与CP交点为M,又 ,则t=
,则t=
- A.

- B.

- C.

- D.

C
分析:先根据向量关系 得
得 即P是AB的一个三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
即P是AB的一个三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
结合向量条件即可求得t值.
解答: 解:∵
解:∵
∴
∴ 即P是AB的一个三等分点,
即P是AB的一个三等分点,
过点Q作PC的平行线交AB于D,
∵Q是BC中点,∴QD= PC,且D是PB的中点,
PC,且D是PB的中点,
从而QD=2PM,
∴PC=4PM,
∴CM= CP,
CP,
又 ,则t=
,则t=
故选C.
点评:本小题主要考查向量在几何中的应用、两个向量的加减法的法则,以及其几何意义,利用向量的加法的法则,以及其几何意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.
分析:先根据向量关系
 得
得 即P是AB的一个三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,
即P是AB的一个三等分点,利用平面几何知识,过点Q作PC的平行线交AB于D,利用三角形的中位线定理得到PC=4PM,结合向量条件即可求得t值.
解答:
 解:∵
解:∵
∴

∴
 即P是AB的一个三等分点,
即P是AB的一个三等分点,过点Q作PC的平行线交AB于D,
∵Q是BC中点,∴QD=
 PC,且D是PB的中点,
PC,且D是PB的中点,从而QD=2PM,
∴PC=4PM,
∴CM=
 CP,
CP,又
 ,则t=
,则t=
故选C.
点评:本小题主要考查向量在几何中的应用、两个向量的加减法的法则,以及其几何意义,利用向量的加法的法则,以及其几何意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
在△ABC中,点P是BC上的点
=2
,
=λ
+μ
,则( )
| BP |
| PC |
| AP |
| AB |
| AC |
| A、λ=2,μ=1 | ||||
| B、λ=1,μ=2 | ||||
C、λ=
| ||||
D、λ=
|
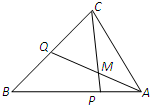 如图,在△ABC中,点P是AB上的一点,且
如图,在△ABC中,点P是AB上的一点,且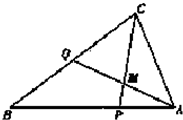 (2010•武汉模拟)在△ABC中,点P是AB上一点,且
(2010•武汉模拟)在△ABC中,点P是AB上一点,且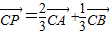 ,Q是BC的中点,AQ与CP交于点M,设
,Q是BC的中点,AQ与CP交于点M,设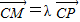 ,
,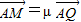 则实数λ+μ=( )
则实数λ+μ=( )