题目内容
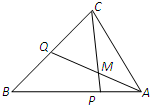如图，在△ABC中，点P是AB上的一点，且| CP |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
| CM |
| CP |
| AM |
| AQ |
分析：由已知中在△ABC中，点P是AB上的一点，且
=
+
，Q是BC的中点，AQ与CP交于点M，设
=λ
，
=μ
，根据三点共线的充要条件，我们易构造关于λ和μ的方程，并分别求出λ和μ的值，进而得到答案．
| CP |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
| CM |
| CP |
| AM |
| AQ |
解答：解：∵
=
+
=
+
化简得：
=
=
即P为BA的三等分点，
∴
=
∵
=μ
=μ•
（
+
）=
+
∵C，M，P三点共线
∴
+
=1
解得μ=
又∵
=λ
=
+
=
+
，
∵A，M，Q三点共线
∴
+
=1
解得λ=
故λ+μ=
故选C．
| CP |
| CB |
| BP |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
化简得：
| BP |
| 2 |
| 3 |
(
|
| 2 |
| 3 |
| BA |
即P为BA的三等分点，
∴
| AP |
| 1 |
| 3 |
| AB |
∵
| AM |
| AQ |
| 1 |
| 2 |
| AB |
| AC |
| 3μ |
| 2 |
| AP |
| μ |
| 2 |
| AC |
∵C，M，P三点共线
∴
| 3μ |
| 2 |
| μ |
| 2 |
解得μ=
| 1 |
| 2 |
又∵
| CM |
| CP |
| 2λ |
| 3 |
| CA |
| λ |
| 3 |
| CB |
| 2λ |
| 3 |
| CA |
| 2λ |
| 3 |
| CQ |
∵A，M，Q三点共线
∴
| 2λ |
| 3 |
| 2λ |
| 3 |
解得λ=
| 3 |
| 4 |
故λ+μ=
| 5 |
| 4 |
故选C．
点评：本题考查的知识点是向量在几何中的应用，三点共线的充要条件，其中当A，B，P三共线时，若O这直线外一点，且
=λ
+μ
，则λ+μ=1，是解答本题的关键．
| OP |
| OA |
| OB |
练习册系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知